Thế năng là gì? Lý thuyết và công thức tính thế năng

Thế năng là một trong những kiến thức quan trọng về cơ học trong chương trình Vật Lý lớp 10. Nắm được kiến thức về thế năng và các công thức tính toán sẽ giúp các em học sinh giải quyết các bài toán về động năng, thế năng và cơ năng nhanh chóng và chính xác. Vậy thế năng là gì? Công thức tính thế năng trọng trường và đàn hồi như thế nào? Các em hãy cùng Team Marathon Education tìm hiểu ngay những kiến thức này qua bài viết sau.

Thế năng là gì?

Thế năng là một trong những đại lượng vật lý quan trọng. Đại lượng này biểu hiện khả năng sinh công của một vật trong một số điều kiện nhất định. Nói cách khác, thế năng chính là một dạng năng lượng tồn tại bên trong vật thể. Có 3 loại thế năng: thế năng trọng trường, thế năng đàn hồi và thế năng tĩnh điện.

Tuy nhiên, trong chương trình Vật Lý lớp 10, các em sẽ chỉ tập trung tìm hiểu về 2 loại thế năng phổ biến. Đó là thế năng trọng trường và thế năng đàn hồi. Mỗi loại đều có khái niệm, đặc điểm và công thức tính toán riêng.

Thế năng trọng trường là gì? Công thức tính thế năng trọng trường

Khái niệm thế năng trọng trường

Thế năng trọng trường gắn liền với trọng trường của Trái Đất. Trước khi tìm hiểu thế năng trọng trường là gì, Team Marathon Education sẽ giải thích cho các em hiểu về trọng trường của Trái Đất và tác động của nó đối với các vật thể bên trong.

Trọng trường là môi trường tồn tại xung quanh Trái Đất. Mọi vật thể bên trong trọng trường của Trái Đất đều bị tác động bởi lực hấp dẫn (trọng lực). Công thức tính trọng lượng của một vật có khối lượng m được đặt trong trọng trường:

P = m.g

Trong đó:

• P là trọng lượng, đơn vị đo là Newton (N)
• m là khối lượng của vật thể, đơn vị đo là kg
• g là gia tốc rơi tự do hay gia tốc trọng trường, đơn vị đo là m/s²

Từ đó, ta có thể định nghĩa thế năng trọng trường của một vật bất kỳ chính là năng lượng vật có được khi có lực hấp dẫn giữa vật và Trái Đất. Độ lớn của thế năng trọng trường phụ thuộc vào vị trí của vật thể bên trong trọng trường.

Công thức tính thế năng trọng trường

Thế năng trọng trường của một vật thể bất kỳ có khối lượng m đặt ở vị trí cách mốc thế năng một khoảng z trong môi trường trọng trường, được tính theo công thức sau:

W_t =m.g.z

Trong đó

• W_t là thế năng trọng trường của thể vật tại vị trí đang xét, đơn vị đo là J (Jun)
• m là khối lượng của vật thể, đơn vị đo là kg
• z là khoảng cách từ vật đến mốc thế năng, đơn vị đo là m
• g là độ lớn gia tốc rơi tự do của vật thể, đơn vị đo là m/s²

Mốc thế năng là vị trí ban đầu của vật trong trọng trường trước khi sinh công. Ví dụ như khi vật được ném lên không trung, lúc này, vị trí vật được ném lên chính là mốc thế năng.

Các trường hợp có thể xảy ra là:

• W_t > 0
• W_t = 0
• W_t < 0
• z > 0 khi vật ở trên mốc thế năng.
• z <0 khi vật ở dưới mốc thế năng.

Sự biến thiên hay sự thay đổi của thế năng và công của trọng lực phụ thuộc vào vị trí của vật ở các thời điểm khác nhau. Khi vật thể di chuyển từ vị trí M đến vị trí N trong trọng trường (tăng độ cao hoặc giảm độ cao), công của trọng lực sẽ bằng với hiệu thế năng giữa 2 vị trí và được tính theo công thức A_MN = W_t(M) – W_t(N).

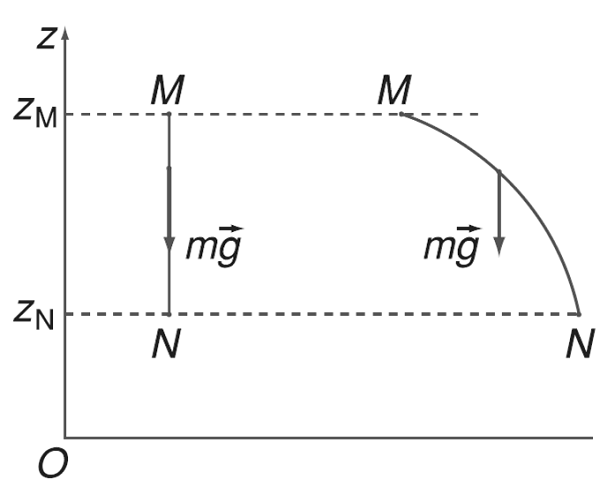
Thế năng đàn hồi là gì? Công thức tính thế năng đàn hồi

Khái niệm thế năng đàn hồi

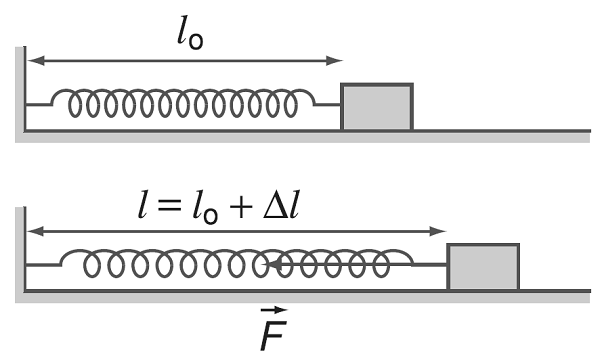
Một vật bị biến dạng do lực tác động từ bên ngoài và sinh công. Khi đó, năng lượng sinh ra được gọi là thế năng đàn hồi.

Xét một lò xo có một đầu cố định, một đầu gắn vào một vật có trọng lượng m. Lò xo có độ cứng k và có chiều dài tự nhiên l₀. Khi bị kéo dãn một đoạn Δl, độ dài lò xo vào thời điểm đó là l = l₀ + Δl.

Lúc đó, theo định luật Hooke, sẽ xuất hiện một lực đàn hồi có độ lớn là F = k.|Δl|. Lực này tác động vào lò xo nhằm đưa lò xo về trạng thái cân bằng. Công của lực đàn hồi này sẽ được tính theo công thức:

 A=\frac{1}{2}k(Δl)^2

Công thức tính thế năng đàn hồi

Công thức tính thế năng đàn hồi khi lò xo bị biến dạng một đoạn Δl là:

W_t=\frac{1}{2}k(Δl)^2

Trong đó:

• W_t là thế năng đàn hồi, đơn vị đo là J (Jun)
• k là độ cứng của lò xo, đơn vị đo là N.m
• ∆l là độ biến dạng của lò xo, đơn vị đo là m

Bài tập vận dụng

Bài tập 1 (Bài 3 Trang 141 SGK Lý 10)

Một vật có khối lượng 1,0 kg có thế năng 1,0 J đối với mặt đất. Lấy g = 9,8 m/s². Khi đó, vật ở độ cao bao nhiêu so với mặt đất?

Lời giải:

\begin{aligned}
& \small \text{Dựa trên công thức tính thế năng trọng trường: } W_t = mgz
\\
& \small \iff z = \frac{W_t}{mg} = \frac{1}{1.9,8} = 0,102 \ m
\end{aligned}

Bài tập 2 (Bài 6 Trang 141 SGK Lý 10)

Một lò xo có độ cứng k = 200 Nm, một đầu cố định đầu kia gắn với vật nhỏ. Khi bị lò xo nén 2 cm thì thế năng đàn hồi của hệ bằng bao nhiêu? Thế năng này có phụ thuộc khối lượng của vật không?

Lời giải:

\begin{aligned}
& \small \text{Thế năng đàn hồi của lò xo trong hệ: }
\\
& \small W_t = \frac12k(Δl)^2 = \frac12.200.(2.10^{-2})^2 = 0,04 \ J
\\
& \small \text{Thế năng này không phụ thuộc vào khối lượng của vật.}
\end{aligned}

Bài tập 3

Một người có khối lượng 60kg đứng trên mặt đất và cạnh một giếng nước, lấy g = 10 m/s².

a. Tính thế năng của người đó tại vị trí A cách mặt đất 3m về phía trên và tại đáy giếng cách mặt đất 5m, lấy gốc thế năng tại mặt đất.

b. Với mốc thế năng tại đáy giếng, hãy tính lại kết quả câu a

c. Tính công của trọng lực nếu người này di chuyến từ đáy giếng lên độ cao 3m so với mặt đất. Nhận xét kết quả thu được.

Lời giải:

\begin{aligned}
& \small \text{a. }
\\
& \small \text{Lấy vị trí mặt đất làm gốc thế năng: }
\\
& \small \text{Thế năng người đó tại vị trí A cách mặt đất 3m về phía trên: } 
\\
& \small W_{t_A} = mgz_A = 60.10.3 = 1800 \ J
\\
& \small \text{Gọi B là vị trí tại đấy giếng cách mặt đất 5m. Thế năng tại vị trí B: }
\\
& \small W_{t_B} = -mgz_B = -60.10.5 = -3000 \ J
\\
& \small \text{b. }
\\
& \small \text{Lấy vị trí đáy giếng làm gốc thế năng.}
\\
& \small \text{Thế năng người đó tại vị trí A cách mặt đất 3m về phía trên: }
\\
& \small W_{t_A} = mgz_A = 60.10.(3 + 5) = 4800 \ J
\\
& \small \text{Thế năng tại vị trí B: }
\\
& \small W_{t_B} = -mgz_B = 60.10.0 = 0 \ J
\\
& \small \text{c. }
\\
& \small \text{Công của trọng lực nếu người này di chuyến từ đáy giếng lên độ cao 3m so với mặt đất: }
\\
& \small A = W_{t_B} - W_{t_A} = 0 - 4800 = - 4800 \ J < 0
\\
& \small \text{Công của trọng lực là công âm vì A < 0.}
\end{aligned}

Bài tập 4

Một học sinh lớp 10 trong giờ Vật Lý làm thí nghiệm thả một quả cầu có khối lượng 250 g từ độ cao 1,5 m so với mặt đất. Tính độ cao của vật so với mặt đất khi vận tốc 18 km/h. Chọn vị trí thả vật làm gốc thế năng. Lấy g = 10m/s².

Lời giải:

\begin{aligned}
& \small \text{Đổi đơn vị: } 18 \ km/h = 5 \ m/s, 250 \ g = 0,25 \ kg
\\
& \small \text{Theo định lý động năng ta có: } A = W_d = \frac12mv^2 = \frac12.0,25.5^2 = 3,125 \ J
\\
& \small \text{Theo định lý thế năng ta có: } A = -W_t = -mgz
\\
& \small \iff z = \frac{A}{mg} = \frac{3,125}{0,25.10} = 1,25 \ m
\\
& \small \text{Độ cao của vật so với mặt đất khi vận tốc 18 km/h: } h = h_0 - z = 1,5 - 1,25 = 0, 25 \ m
\end{aligned}

Bài tập 5

Một xe có khối lượng m = 2,8 kg chuyển động theo quỹ đạo cong như hình vẽ. Độ cao của các điểm A, B, C, D, E được tính đối với mặt đất và có các giá trị: h_A = 6 m, h_B = 3 m, h_C = 4 m, h_D = 1,5 m, h_E = 7 m. Lấy g = 10 m/s². Tính độ biến thiên thế năng của xe trong trọng lượng khi nó di chuyển từ:

a. Từ A đến B.

b. Từ B đến C.

c. Từ A đến D.

d. Từ A đến E.

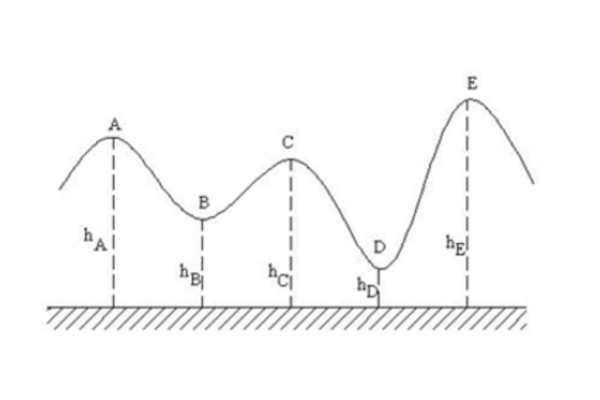
Lời giải:

a. Từ A đến B: ΔW_t = m.g.(h_B– h_A ) = 2,8.10.(3- 6)= -84J ⇒ thế năng giảm.

b. Từ B đến C: ΔW_t = m.g.(h_C – h_B ) = 2,8.10.(4 – 3)= 28J

c. Từ A đến D: ΔW_t = m.g.(h_D – h_A ) = 2,8.10.(1,5 – 6)= -126J ⇒ thế năng giảm.

d. Từ A đến E: ΔW_t = m.g.(h_E – h_A ) = 2,8.10.(7 – 6) = 28J

Bài tập 6

Một vật nhỏ có khối lượng m=160 g gắn vào đầu của một lò xo đàn hồi có độ cứng k=100 N/m, khối lượng không đáng kể; đầu kia của của lò xo được giữ cố định. Tất cả nằm trên một mặt ngang không ma sát. Vật được đưa về vị trí mà tại đó lò xo dãn 5 cm. Sau đó vật được thả nhẹ nhàng. Dưới tác dụng của lực đàn hồi, vật bắt đầu chuyển động. Xác định vận tốc của vật khi:

a) Vật về tới vị trí lò xo không biến dạng.

b) Vật về tới vị trí lò xo dãn 3 cm.

Lời giải:

Chọn mốc thế năng và gốc tọa độ tại vị trí lò xo không biến dạng, chiều dương của trục tọa độ trùng chiều lò xo dãn.

\begin{aligned}
& \small \text{a) Tại vị trí lò xo không biến dạng:}
\\
& \small \text0,5kx_o^2=0,5mv_o^2\Rightarrow |v_o|=\sqrt{\frac{k}{m}}|x_o|=1,25m/s=125cm/s\\
& \small \text{b) Tại vị trí lò xo dãn 3cm}\\
& \small \text 0,5kx_0^2=0,5mv^2+0,5kx^2\Rightarrow v=\sqrt{\frac{k}{m}(x_0^2-x^2)}=1m/s
\end{aligned}

Bài tập 7

Một cần cẩu nâng một thùng hàng có khối lượng 420 kg từ mặt đất lên độ cao 3 m ( tính theo di chuyển khối tâm của thùng), sau đó đổi hướng và hạ thùng này xuống sàn một ô tô tải ở độ cao 1.25 m so với mặt đất.

a. Tìm thế năng của thùng trong trọng trường khi ở độ cao 3 m. Tính công của lực phát động (lực căng của dây cáp) để nâng thùng hàng lên độ cao này.

b. Tìm độ biến thiên thế năng khi hạ thùng từ độ cao 3 m xuống sàn ô tô. Công của trọng lực có phụ thuộc cách di chuyển thùng giữa hai vị trí đó hay không? Tại sao?

Lời giải:

a. Thế năng của thùng: W_t = mgz = 420.10.3 = 12600 (J).

Coi thùng được nâng đều, lực phát động có độ lớn bằng trọng lực. Độ giảm thế năng bằng công của trọng lực: W_t – 0 = – A_P.

Công của lực phát động: A_F = – A_P = W_t = 12600 (J).

b. Độ biến thiên thế năng khi hạ thùng xuống sàn ô tô:

W = W₂ – W₁ = mg(h₂ – h₁ ) = 420.10.(1,25-3) = -7350 (J)

=> Trong trường hợp này thế năng giảm.

Công của trọng lực không phụ thuộc vào cách di chuyển thùng giữa hai vị trí vì trọng lực là lực thế, công của nó chỉ phụ thuộc vào mực chênh lệch độ cao giữa hai vị trí đầu và cuối mà không phụ thuộc vào dạng đường đi.

Bài tập 8 (trang 171 SGK Vật Lý 10 nâng cao)

Giữ một vật khối lượng 0.25 kg ở đầu một lò xo đặt thẳng đứng với trạng thái ban đầu chưa bị biến dạng. ấn cho vật đi xuống làm lò xo bị biến dạng một đoạn 10 cm. Tìm thế năng tổng cộng của hệ vật – lò xo tại vị trí này. Lò xo có độ cứng 500N/m và bỏ qua khối lượng của nó. Cho g = 10 m/s² và chọn mức không của lò xo tại vị trí lò xo không biến dạng.

Lời giải:

Chọn mốc thế năng tại vị trí lò xo không biến dạng

– Thế năng đàn hồi của vật tại vị trí lò xo bị nén một đoạn 10 cm xuống phía dưới là:

\begin{aligned}
&W_{đh}=\frac{kx^2}{2} = \frac{1}{2} . 500 . 0,1^2 = 2,5J
\end{aligned}

– Tại vị trí trên, thế năng trọng trường của vật là: W_t = mgz = 0,25.10.(-0,1) = -0,25J

– Vậy thế năng tổng cộng của hệ vật – lò xo tại vị trí lò xo bị nén 10cm xuống phía dưới là:

W_đh+ W_t = 2,5 + (-0,25) = 2,25J

Bài tập 9

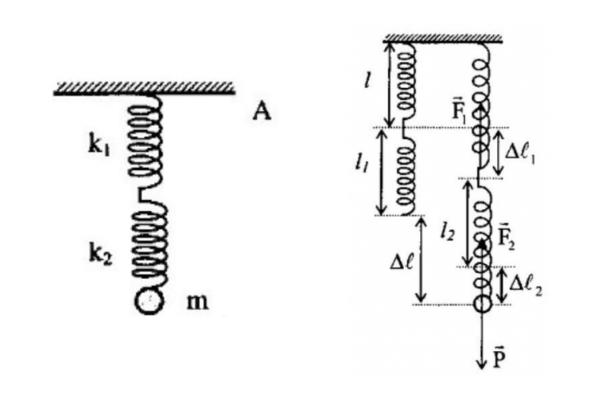
Hai lò xo k₁ = 0.2 N/cm; k₂ = 0.6 N/cm nối với nhau và nối với điểm cố định A, vật m = 150g treo ở đầu hai lò xo (hình vẽ).

a/ Tính độ biến dạng của mỗi lò xo tại vị trí cân bằng O.

b/ Kéo m lệch khỏi vị trí cân bằng đoạn x = 2 cm. Tính thế năng đàn hồi của hệ hai lò xo tại vị trí x. Chọn gốc thế năng tại vị trí cân bằng.

Lời giải:

\begin{aligned}
& \small \text{a) Khi cân bằng, lò xo 1 và 2 lần lượt bị dãn đoạn}\ {Δl}_1 \ và \  {Δl}_2
\\
&\small \text {- Điều kiện cân bằng:}\ {k}_1{Δl}_1 = {k}_2{Δl}_2 = mg
\\ 
&\Rightarrow{Δl}_1 = \frac{mg}{{k}_1} = \frac{0,15.10}{0,2} = 7,5cm; {Δl}_2 = \frac{mg}{{k}_2} = \frac{0,15.10}{0,6} = 2,5cm
\\
&\small \text {Vậy, khi cân bằng lò xo 1 dãn 7,5cm và lò xo 2 dãn 2,5cm.}\ 
\\
&\small \text {b) Khi cân bằng lò xo 1 và lò xo 2 dãn một đoạn lần lượt là}\ {Δl}_1 \ và \  {Δl}_2.
\\
&\small \text {Đồng thời, hệ lò xo dãn đoạn}\ {Δl}.\Rightarrow{Δl}={Δl}_1 +{Δl}_2
\\
&\small \text {Gọi k là độ cứng của hệ lò xo, ta có: }mg=k{Δl}
\\
&\small \text {- Ta có phương trình sau: }
\\
&mg=k({Δl}_1+{Δl}_2)=k\bigg(\frac{mg}{k_1}+\frac{mg}{k_2}\bigg)=mgk\bigg(\frac{1}{k_1}+\frac{1}{k_2}\bigg)
\\
&\Rightarrow\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}\Rightarrow{k}=\frac{k_1.k_2}{k_1+k_2}=\frac{0,2.0,6}{0,2+0,6}=0,15 N/cm=15N/m
\\
&\small \text {- Thế năng của hệ ở vị trí x=2cm=0,02m là: }
\\
&W_t=\frac{1}{2}.kx^2=\frac{1}{2}.15.{0,02^2}=0,003J=3mJ
\end{aligned}

Tham khảo ngay các khoá học online của Marathon Education

Qua bài viết trên, Team Marathon đã tổng hợp lại cho các em những kiến thức về thế năng là gì cũng như các công thức tính thế năng trọng trường và thế năng đàn hồi. Quá đơn giản và dễ nhớ phải không nào! Hy vọng bài viết sẽ giúp các em nắm rõ kiến thức này và vận dụng tốt vào bài tập liên quan. 

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!