Suất điện động cảm ứng, định luật Faraday và Len-xơ
Suất điện động cảm ứng là một trong những kiến thức quan trọng trong chương trình Vật lý lớp 11. Khi nắm vững kiến thức này và các định luật liên quan, các bài tập về điện sẽ trở nên dễ dàng hơn rất nhiều. Trong bài viết dưới đây, Team Marathon Education đã tổng hợp lý thuyết và những kiến thức cơ bản về suất điện động cảm ứng, định luật Faraday và định luật Len-xơ giúp các em ghi nhớ dễ dàng hơn.
Suất điện động cảm ứng là gì?
Trong mạch điện kín (ký hiệu là C), suất điện động cảm ứng là suất điện động sinh ra dòng điện cảm ứng. Suất điện động cảm ứng trong vật lý ký hiệu là ec, đơn vị tính là vôn (V).
Nội dung định luật Faraday
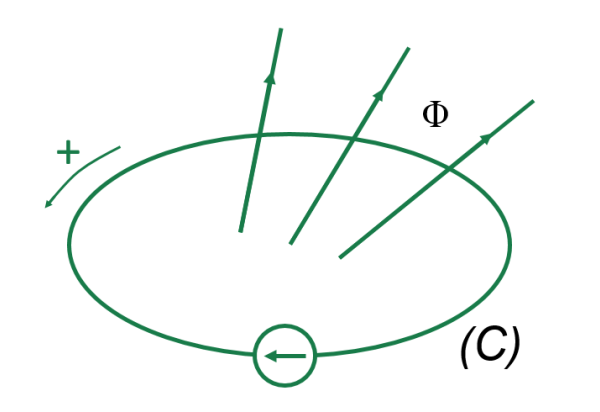
Một mạch kín (C) với từ trường không đổi có sự thay đổi của dòng điện khiến từ thông qua mạch biến thiên một đại lượng ∆Φ trong khoảng thời gian ∆t. Trong trường hợp này:
- Lực tương tác tác dụng lên mạch (C) sinh ra một công ∆A. Công thức: ∆A = i∆Φ (i là cường độ dòng điện cảm ứng).
- Dựa trên định luật Len-xơ, để gây biến thiên từ thông trong mạch, công ngoại lực sinh ra sẽ là ∆A’ = -∆A = -i∆Φ (1).
- Công “∆A’” có độ lớn bằng phần năng lượng do bên ngoài cung cấp cho mạch (C) và được chuyển hóa thành điện năng của suất điện động cảm ứng ec là: ∆A’ ’ = eci∆t (2).
Kết hợp 2 phương trình (1) và (2), công thức tính suất điện động cảm ứng là:
ec = -∆Φ ∆t (3)
Nếu chỉ xét độ lớn thì |ec| = |∆Φ ∆t|
Từ các công thức nêu trên, định luật Faraday có thể được hiểu là: Độ lớn suất điện động cảm ứng xuất hiện trong một mạch kín bất kì thì tỉ lệ với tốc độ biến thiên từ thông sinh ra trong mạch kín đó.
Quan hệ giữa định luật Len-xơ và suất điện động cảm ứng
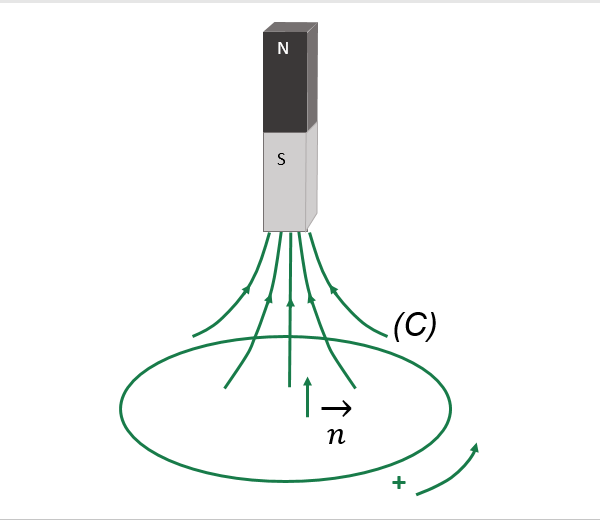
Trong trường hợp này, trước tiên các em cần phải định hướng mạch kín (C). Sau đó, các em căn cứ vào chiều pháp tuyến dương để tính từ thông Φ qua mạch kín (C) (Φ là một đại lượng đại số).
- Trong trường hợp Φ tăng thì ec < 0. Khi đó, chiều của suất điện động cảm ứng ngược chiều với chiều của mạch (C).
- Ngược lại nếu giảm Φ giảm thì ec > 0. Khi đó, chiều của suất điện động cảm ứng cùng chiều với chiều của mạch (C).
Sự chuyển hóa năng lượng trong hiện tượng cảm ứng điện từ
Giả sử ta có mạch kín với từ trường không đổi, nếu muốn tạo ra sự biến thiên từ thông thì cần phải có một ngoại lực tác dụng vào mạch tạo nên sự dịch chuyển trong mạch. Khi đó, ngoại lực này sẽ sinh ra một công cơ học. Lúc này, công cơ học từ ngoại lực này đã tạo nên sự xuất hiện suất điện động cảm ứng trong mạch hay nói cách khác là tạo ra điện năng. Trong thí nghiệm này sự chuyển hóa năng lượng là quá trình chuyển hóa cơ năng thành điện năng.
>>> Xem thêm: Hiện Tượng Cảm Ứng Điện Từ Là Gì? Lý Thuyết Về Cảm Ứng Điện Từ
Ứng dụng của hiện tượng cảm ứng điện từ
- Máy phát điện một chiều
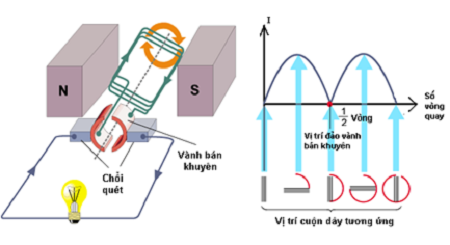
- Máy phát điện xoay chiều
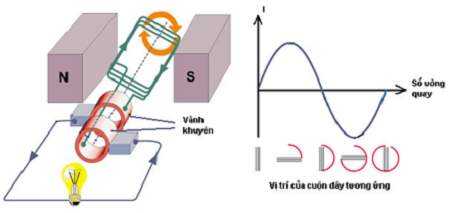
Bài tập vận dụng
Bài tập 1: Một mạch kín hình vuông, cạnh 10 cm , đặt vuông góc với một từ trường đều có độ lớn thay đổi theo thời gian. Tính tốc độ biến thiên của từ trường, biết cường độ dòng điện cảm ứng i = 2 A và điện trở của mạch r = 5 Ω.
Lời giải:
\begin{aligned}
& \text{Ta có:}
\\
& e_c = ri = 5.2 = 10 V
\\
& e_c = |\frac{ΔΦ}{Δt}| = \frac{ΔB}{Δt}.S
\\
⇔\ &\frac{ΔB}{Δt} = \frac{e_c}{S} = \frac{10}{0,1^2} = 10^3 \ T/s
\end{aligned}
Bài tập 2: Một khung dây dẫn hình vuông, cạnh a = 10 cm, đặt cố định trong một từ trường đều có vec tơ cảm ứng từ vuông góc với mặt khung. Trong khoảng thời gian = 0,05 s cho độ lớn của tăng đều từ 0 đến 0,5 T. Xác định độ lớn của suất điện động cảm ứng xuất hiện trong khung.
Lời giải:
\begin{aligned}
& \text{Ta có:}
\\
& ΔΦ = ΔBS = ΔBa^2
\\
& |e_c| = |\frac{ΔΦ}{Δt}| = \frac{0,5}{0,05}.0,1^2 = 0,1 \ V
\end{aligned}
Bài tập 3. Một khung dây phẳng diện tích 20 cm2, gồm 10 vòng được đặt trong từ trường đều. Véc tơ cảm ứng từ làm thành với mặt phẳng khung dây góc 30o và có độ lớn bằng 2.10−4T. Người ta làm cho từ trường giảm đều đến 0 trong thời gian 0,01 s. Tính suất điện động cảm ứng xuất hiện trong khung dây trong thời gian từ trường biến đổi.
Lời giải:
\begin{aligned}
& \text{Ta có:}
\\
& Φ_1 = NBScosα = 10.2.10^{-4}.20.cos(90^o-30^o) = 2.10^{-6} \ V
\\
&Φ_2 = 0
\\
⟹\ & ΔΦ = Φ_1 - Φ_2 = 2.10^{-6} \ V
\\
&|e_c| = |\frac{ΔΦ}{Δt}| = \frac{2.10^{-6}}{0,01} = 2.10^{-4} \ V
\end{aligned}
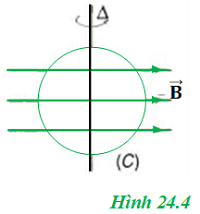
Bài tập 4: Một mạch kín tròn (C) bán kính R, đặt trong từ trường đều, trong đó vectơ cảm ứng từ B lúc đầu có hướng song song với mặt phẳng chứa (C) (hình 24.4). Cho (C) quay đều xung quanh trục Δ cố định đi qua tâm của (C) và nằm trong mặt phẳng chứa (C); tốc độ quay là ω không đổi. Xác định suất điện động cảm ứng cực đại xuất hiện trong (C).
Lời giải:
\begin{aligned}
& \small \text{Trong mạch (C), xuất điện động cảm ứng: } e_C = \frac{ΔΦ}{Δt} = -Φ'(t) \text{ (khi Δt rất nhỏ)}
\\
& \small Φ(t) = B.S.cosα = B.S.cos(ωt + φ)
\\
& \small \text{Φ là góc hợp bởi véctơ pháp tuyến khung dây n và cảm ứng từ B tại thời điểm ban đầu khi t = 0.}
\\
& \small \text{Lúc đó } e_C = -Φ'(t) = N.B.S.ω.sin(ωt + φ)
\\
& \small \implies (e_C)_{max} = B.S.ω = B.ω.π.R^2
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Trên đây là những lý thuyết cơ bản về suất điện động cảm ứng, mối quan hệ với định luật Len-xơ và định luật Faraday mà Team Marathon đã tổng hợp và chia sẻ. Hy vọng bài viết sẽ giúp các em vận dụng kiến thức này vào các bài tập tốt hơn. Hãy thường xuyên theo dõi Marathon Education để học online thật nhiều kiến thức Toán – Lý – Hóa cấp 3 các em nhé!






