Động Lượng Là Gì? Định Luật Bảo Toàn Động Lượng

Động lượng là một trong những phần kiến thức tương đối khó trong chương trình Vật Lý lớp 10. Tuy nhiên, nội dung này thường xuất hiện khá nhiều trong các đề kiểm tra. Vì thế, để giúp các em tìm hiểu thật kỹ về động lượng và định luật bảo toàn động lượng, Marathon Education đã tổng hợp những kiến thức liên quan và chia sẻ đến các em qua bài viết bên dưới đây. 

Động lượng

Động lượng là gì?

Động lượng của chất điểm được định nghĩa là đại lượng vectơ xác định bằng tích khối lượng với vận tốc của chất điểm đó. 

Công thức tính động lượng được biểu diễn: p=mv

Đơn vị của động lượng

Đơn vị: kg.m/s

Xung lượng của lực

Trong trường hợp một lực F tác dụng lên một vật bất kỳ nào đó trong khoảng thời gian t thì F.t sẽ biểu thị cho xung lượng của lực F này trong khoảng thời gian đã đề cập ấy. 

Cách phát biểu khác của định luật II Newton

Giữa động lượng và xung lượng của vật có mối quan hệ trực tiếp với nhau và được biểu diễn cụ thể bằng phương trình sau: p=F.t.

Trong đó:

 t: độ biến thiên thời gian (s)

p: Độ biến thiên động lượng (kg.m/s)

F: lực tác dụng lên vật (N)

Khi có một lực đủ mạnh tác dụng lên một vật bất kỳ trong khoảng thời gian cụ thể thì sẽ khiến cho động lượng của vật xảy ra sự biến thiên.

Định luật bảo toàn động lượng

Dưới đây là định luật bảo toàn động lượng quan trọng mà các em cần ghi nhớ cũng như hiểu thật rõ để có thể vận dụng vào giải các bài tập liên quan đến phần kiến thức này. 

Hệ cô lập

Một hệ bất kỳ được gọi là hệ cô lập khi và chỉ khi không có ngoại lực tác dụng lên hệ hoặc nếu có thì các ngoại lực này cân bằng với nhau. 

Trong hệ cô lập chỉ tồn tại các nội lực và các lực này tương tác giữa các vật có trong hệ trực đối với nhau theo từng đôi một. 

Định luật bảo toàn động lượng của hệ cô lập

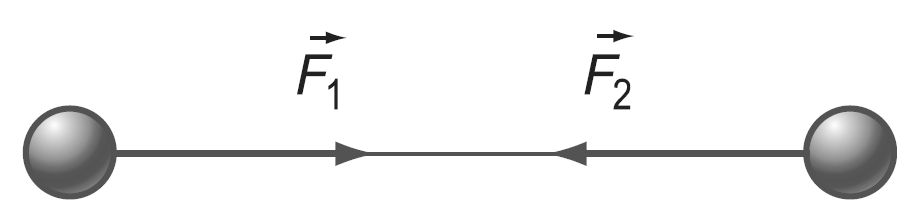
Động lượng của một hệ cô lập là đại lượng được bảo toàn: p1+p2+pn=không đổi.

Biểu thức của định luật ứng với hệ cô lập bao gồm hai vật là m1 và m2 sẽ được biểu diễn như sau: p1+p2=const hay m1V1+m2V2=m1V1’+m2V2′

Trong đó: m1V1 và m2V2chính là động lượng của vật 1 và vật 2 trước khi xảy ra tương tác. m1V1′ và m2V2’là động lượng của vật 1 và vật 2 sau khi xảy ra tương tác. 

Va chạm mềm

Va chạm mềm là va chạm không đàn hồi, sau va chạm hai vật gắn chặt vào nhau và chuyển động cùng với vận tốc giống nhau. 

Lúc này, theo định luật bảo toàn động lượng, ta có: m1V1=(m1+m2)vv=m1V1m1+m2.

Va chạm của hai vật diễn ra như vậy sẽ được gọi là va chạm mềm. 

Lưu ý: v1,v2,V là những giá trị có thể âm, dương, hoặc bằng 0 tùy vào từng trường hợp cụ thể và hệ quy chiếu ta chọn.

Một số ứng dụng của định luật bảo toàn động lượng

• Chuyển động bằng phản lực: Trong một hệ kín bất kỳ đứng yên, nếu một phần của hệ này chuyển động theo một hướng bất kỳ thì phần còn lại của hệ bắt buộc chuyển động theo hướng ngược lại. Chuyển động như vậy được gọi là chuyển động bằng phản lực.

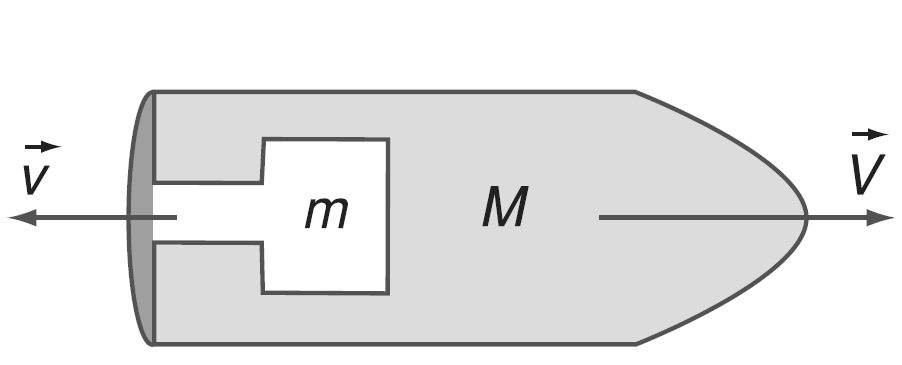
• Súng giật khi bắn: Dựa theo định luật bảo toàn động lượng, trước khi bắn, động lượng của hệ bằng không nên sau khi bắn, ta có V=-mMv. Điều này chứng tỏ súng chuyển động ngược chiều với đạn nên có hiện tượng “giật” xảy ra. 

Bài tập về định luật bảo toàn động lượng

Bài tập 1: Hai hòn bi có khối lượng lần lượt 1kg và 2kg chuyển động trên mặt phẳng nằm ngang ngược chiều nhau với các vận tốc 2m/s và 2,5 m/s. Sau va chạm, hai xe dính vào nhau và chuyển động với cùng vận tốc. Tìm độ lớn và chiều của vận tốc này, bỏ qua mọi lực cản.

Theo định luật bảo toàn động lượng

m₁V₁=(m₁+m₂)v => v=(m₁.V₁) : (m₁+m₂)

v=(1,2-2.2,25)/(1+2)= -1(m/s)

Vậy sau va chạm hai vật chuyển động với vận tốc -1 m/s và chuyển đông ngược chiều so với vận tốc ban đầu của vật một

Bài tập 2: Một búa máy có khối lượng 300kg rơi tự do từ độ cao 31,25m vào một cái cọc có khối lượng 100kg, va chạm giữa búa và cọc là va chạm mềm. Bỏ qua sức cản của không khí lấy g = 10m/s. Tính vận tốc búa và cọc sau va chạm.

Vận tốc của búa trước lúc va chạm với cọc:

v1=2gh=2.10.31,25=25 (m/s)

Chọn chiều dương là chiều chuyển động của búa trước lúc va chạm

Theo định luật bảo toàn động lượng:

m1V1=(m1+m2)v

Chiếu lên chiều dương ta có:

v=m1v1m1+m2= 300.25300+100=18,75(m/s)

Bài tập 4: Một tên lửa khối lượng 70 tấn đang bay với vận tốc 200 m/s đối với trái đất thì tức thời phụt ra lượng khí có khối lượng 5 tấn với vận tốc  450m/s đối với tên lửa. Xác định vận tốc tên lửa sau khi phụt khí ra đối với trái đất.

\begin{aligned}
&\text{Theo định luật bảo toàn động lượng}:\\
&m_ov_o=(m_0-m.V)+m(v_0-v)\\
&V=\frac{m_0v_0-m(v_0.v)}{m_0-m}\\
&v=\frac{70000.200-5000(200-450)}{70000-5000}\approx234,6m/s
\end{aligned}

Tham khảo ngay các khoá học online của Marathon Education

Động lượng là phần kiến thức có hơi phức tạp và đòi hỏi sự tập trung cao để có thể hiểu hết được các phần lý thuyết. Hy vọng bài viết chi tiết bên trên từ Marathon sẽ giúp các em củng cố được phần nào kiến thức về động lượng. Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!