Giao Thoa Sóng Là Gì? Lý Thuyết Và Công Thức Giao Thoa Sóng

Giao thoa sóng là kiến thức quan trọng trong chương trình Vật Lý 12 thường xuất hiện trong các đề thi đại học. Do đó, các em phải hiểu rõ lý thuyết và công thức để từ đó giải tốt các bài tập liên quan. Vậy giao thoa sóng là gì? Có những công thức tính toán nào? Qua bài viết này Team Marathon sẽ giúp các em nắm vững những kiến thức liên quan đến chủ đề này.

>>> Xem thêm: Lý Thuyết Lý 12: Đặc Trưng Vật Lí Của Âm

Giao thoa sóng là gì?

Định nghĩa

Giao thoa sóng là sự tổng hợp của hai sóng kết hợp ở trong không gian, trong đó có những vị trí biên độ sóng bị giảm bớt hay được tăng cường.

Điều kiện

Điều kiện để có giao thoa là phải có sự kết hợp từ hai nguồn sóng có cùng tần số và có hiệu số pha không đổi theo thời gian.

>>> Xem thêm: Lý Thuyết Lý 12: Sóng Cơ Là Gì? Sự Truyền Sóng Cơ

Công thức giao thoa sóng

Ta xét giao thoa của 2 sóng phát ra từ hai nguồn kết hợp S₁ và S₂ cách nhau một khoảng cách l bất kỳ.

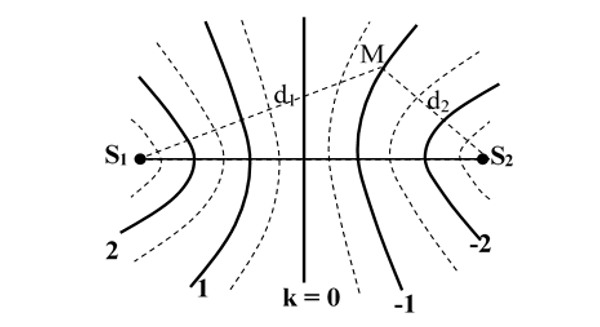
• Phương trình sóng 2 nguồn S₁ và S₂:

u_1=Acos(2\pi ft+\varphi_1)\\
u_2=Acos(2\pi ft+\varphi_2)

• Phương trình sóng tại M cách 2 nguồn S₁ và S₂ khoảng cách d₁ và d₂:

\begin{aligned}
&u_{1M}=Acos\left(2\pi ft+\varphi_1-2\pi \frac{d_1}{\lambda}\right)\\
&u_{2M}=Acos\left(2\pi ft+\varphi_2-2\pi \frac{d_2}{\lambda}\right)\\
&u_M=u_{1M}+u_{2M}=2Acos\left[\pi \frac{d_2-d_1}{\lambda}-\frac{\Delta\varphi}{2} \right]cos\left[2\pi ft-\pi \frac{d_1+d_2}{\lambda}+\frac{\varphi_1+\varphi_2}{2}\right]
\end{aligned}

• Biên độ dao động tại M

A_M=2A\left|cos\left(\pi\frac{d_1-d_2}{\lambda}+\frac{\Delta\varphi}{2}\right)\right| \text{ với }\Delta \varphi=\varphi_2-\varphi_1

• Những điểm dao động với biên độ cực đại

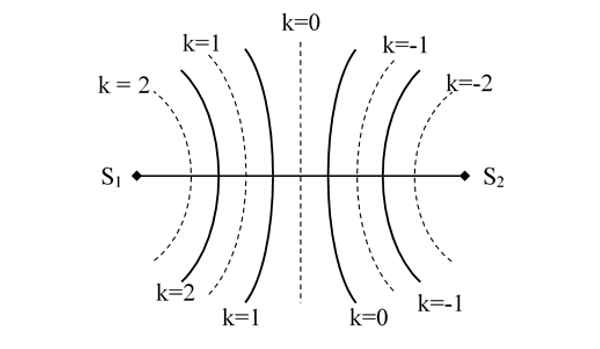
d_e-d_1=k\lambda+\frac{\Delta\varphi}{2\pi}\lambda \text{ với }k=0; \pm1; \pm2; \pm3;...

• Những điểm dao động với biên độ cực tiểu: 

d_2-d_1=\left(k+\frac12\right)\lambda+\frac{\Delta\varphi}{2\pi}\lambda \text{ với }k=0; \pm1; \pm2; \pm3;...

• Lưu ý:

\begin{aligned}
&\small\circ\text{Khoảng cách giữa 2 cực đại hoặc 2 cực tiểu liên tiếp là: } \frac{λ}{2}\\
&\small\circ\text{Khoảng cách gần nhất giữa 1 cực đại và 1 cực tiểu là: }\frac{λ}{4}
\end{aligned}

Hai nguồn dao động cùng pha

Khi hai nguồn sóng dao động cùng pha thì ∆φ = φ₂ – φ₁ = 0 hoặc ∆φ= 2kπ.

• Phương trình giao thoa sóng tại M:

u_M=u_{1M}+u_{2M}=2Acos\left(\pi \frac{d_2-d_1}{\lambda} \right)cos\left(2\pi ft-\pi \frac{d_1+d_2}{\lambda}+\varphi\right)

• Biên độ sóng tổng hợp:

\begin{aligned}
\small\circ\  &\small A_{M\ max} = 2A \text{ khi: Hai sóng thành phần tại M dao động cùng pha với }∆φ = 2kπ\ (k∈Z)\\
&\small \Rightarrow∆d = d_2 – d_1 = kλ\\
\small\circ\  &\small A_{M\ min} = 0 \text{ khi: Hai sóng thành phần tại M dao động ngược pha với }∆φ= (2k + 1)π\ (k ∈ Z).\\
&\small \Rightarrow ∆d = d_2 – d_1 = \left(k + \frac12\right)λ\\
\end{aligned}

• Số điểm dao động cực đại ở trên đoạn S₁S₂:

d_1 – d_2 = kλ\ (k ∈ Z)

Số điểm cực đại là:

-\frac{S_1S_2}{λ} ≤ k ≤ \frac{S_1S_2}{λ} \text{ với }k=0; \pm1; \pm2; \pm3;...

• Số điểm dao động cực tiểu trên đoạn S₁S₂:

d_1 – d_2 = (2k + 1)\frac{λ}{2}\ (k ∈ Z)

Số điểm cực tiểu:

-\frac{S_1S_2}{λ} - \frac12 ≤ k ≤ \frac{S_1S_2}{λ} - \frac12 \text{ với }k=0; \pm1; \pm2; \pm3;...

Như vậy khi hai nguồn dao động cùng pha, cùng biên độ A thì trung điểm I của đoạn S₁S₂ có biên độ cực đại (A _max = 2A) và tập hợp của các điểm cực tiểu, cực đại là các đường Hypebol có S₁, S₂ là tiêu điểm.

Hai nguồn dao động ngược pha 

• Phương trình giao thoa sóng tại M:

u_M=u_{1M}+u_{2M}=2Acos\left(\pi \frac{d_2-d_1}{\lambda} -\pi\right)cos\left(2\pi ft-\pi \frac{d_1+d_2}{\lambda}+\frac{\varphi_1+\varphi_2}{2}\right)

• Biên độ sóng tổng hợp:

A_M=2A\left|cos\left(\pi\frac{d_2-d_1}{\lambda}-\pi\right)\right|

• Điểm dao động cực đại:

d_2 – d_1 = \left(k + \frac12\right)λ\ (k∈Z)

Số điểm hoặc số đường dao động cực đại trên đoạn S₁S₂ (không tính hai nguồn):

-\frac{S_1S_2}{λ} - \frac12 ≤ k ≤ \frac{S_1S_2}{λ} - \frac12 \text{ với }k=0; \pm1; \pm2; \pm3;...

• Điểm dao động cực tiểu (không dao động):

d_2 – d_1 = kl\ (k∈Z)

Số điểm hoặc số đường dao động cực tiểu trên đoạn S₁S₂ (không tính hai nguồn):

-\frac{S_1S_2}{λ} ≤ k ≤ \frac{S_1S_2}{λ} \text{ với }k=0; \pm1; \pm2; \pm3;...

Như vậy khi 2 nguồn dao động ở cùng biên độ A và ngược pha thì trung điểm của S₁S₂ có biên độ (cực tiểu): A_min = 0.

Hai nguồn dao động vuông pha 

• Phương trình giao thoa sóng tại M:

u_M=u_{1M}+u_{2M}=2Acos\left(\pi \frac{d_2-d_1}{\lambda} -\frac{\pi}{4}\right)cos\left(2\pi ft-\pi \frac{d_1+d_2}{\lambda}+\frac{\varphi_1+\varphi_2}{2}\right)

• Biên độ sóng tổng hợp:

A_M=2A\left|cos\left(\pi\frac{d_2-d_1}{\lambda}-\frac{\pi}{4}\right)\right|

• Điểm dao động cực đại:

d_2 – d_1 = \left(k + \frac14\right)λ\ (k∈Z)

• Số điểm hoặc số đường dao động cực đại ở trên đoạn S₁S₂:

-\frac{S_1S_2}{λ} - \frac14 ≤ k ≤ \frac{S_1S_2}{λ} - \frac14\text{ với }k=0; \pm1; \pm2; \pm3;...

• Điểm dao động cực tiểu (không dao động):

d_2 – d_1 = \left(k + \frac34\right)λ\ (k∈Z)

• Số điểm hoặc số đường dao động cực tiểu trên đoạn S₁S₂:

-\frac{S_1S_2}{λ} - \frac34 ≤ k ≤ \frac{S_1S_2}{λ} - \frac34 \text{ với }k=0; \pm1; \pm2; \pm3;...

Như vậy khi cả 2 nguồn dao động ở cùng biên độ A, và vuông pha thì trung điểm của S₁S₂ có biên độ là: A_M = A√2.

Tham khảo ngay các khoá học online của Marathon Education

Trên đây là toàn bộ lý thuyết trọng tâm và công thức của giao thoa sóng trong chương trình Lý 12. Mong những kiến thức tổng hợp này sẽ giúp ích nhiều cho các em trong quá trình ôn luyện và làm bài. 

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!