Lý Thuyết Lý 12: Sóng Cơ Là Gì? Sự Truyền Sóng Cơ

Sóng cơ là kiến thức rất quan trọng mà các em sẽ được học trong năm cuối của chương trình Vật Lý phổ thông. Để giúp các em học hiểu rõ hơn về nội dung này, Marathon Education đã tổng hợp đầy đủ và chi tiết về lý thuyết sóng cơ và sự truyền sóng cơ trong bài viết sau.

>>> Xem thêm: Lý Thuyết Lý 12: Đặc Trưng Vật Lí Của Âm

Sóng cơ là gì?

Định nghĩa

Sóng cơ là sự lan truyền dao động cơ học (bao gồm năng lượng và trạng thái dao động) theo thời gian trong môi trường vật chất đàn hồi.

Ví dụ 1: Cánh bèo hay chiếc phao chỉ dao động trên mặt nước khi sóng truyền qua.

Ví dụ 2: Khi áp tai xuống đường ray, các em có thể nghe thấy tiếng tàu hỏa từ xa đang di chuyển đến mà tại thời điểm đó các em không nghe thấy tàu hỏa trong không khí.

Phân loại sóng cơ

Sóng cơ bao gồm 2 loại là sóng dọc và sóng ngang.

• Sóng dọc: Phương dao động của các phần tử và phương truyền sóng của sóng dọc trùng nhau. Sóng dọc lan truyền được trong môi trường rắn, lỏng và khí. Ví dụ: sóng truyền trên lò xo do sự nén, dãn của lò xo.
• Sóng ngang: Sóng có phương dao động của các phần tử và phương truyền sóng vuông góc với nhau. Sóng ngang chỉ lan truyền được trong môi trường chất rắn, bề mặt chất lỏng và không lan truyền được trong chất lỏng, chất khí. Ví dụ: sóng được lan truyền trên mặt nước.

>>> Xem thêm: Giao Thoa Sóng Là Gì? Lý Thuyết Và Công Thức Giao Thoa Sóng

Các đại lượng của sóng cơ

Biên độ của sóng cơ (A): biên độ dao động của một phần tử vật chất khi sóng truyền qua.

Tần số sóng cơ (f): tần số dao động của một phần tử vật chất khi sóng truyền qua. Công thức tính tần số sóng:

 f = \frac{1}{T} = \frac{ω}{2π}\ (Hz)

Vận tốc sóng cơ (v): vận tốc lan truyền của sóng trong không gian. Công thức tính vận tốc:

v = \frac{ΔS}{Δt}

Trong đó:

• ΔS là quãng đường sóng truyền
• Δt là thời gian sóng truyền

Năng lượng sóng cơ (E_i): năng lượng dao động của các phần tử vật chất tại một điểm khi sóng truyền qua. Công thức tính năng lượng sóng cơ là:

E_i = D. ω^2.\frac{A_i^2}{2}

Trong đó:

• D là khối lượng riêng của môi trường sóng
• A_i là biên độ sóng tại một điểm
• ω là tần số góc của sóng

Bước sóng (λ): là quãng đường mà sóng truyền được trong một chu kỳ cũng chính là khoảng cách của 2 điểm gần nhất trên phương truyền sóng khi dao động cùng pha. Công thức tính bước sóng:

 λ = v.T = \frac{v}{f}\ (m)

Sự truyền sóng cơ

Sự truyền sóng cơ là quá trình lan truyền dao động và năng lượng dao động, phần tử vật chất không có sự truyền đi. Thực tế, sự truyền sóng cơ phụ thuộc vào nhiều yếu tố của môi trường xung quanh.

Trong quá trình truyền sóng cơ:

• Sóng dọc: Các phần tử chỉ dao động theo phương ngang.
• Sóng ngang: Các phần tử chỉ dao động lên xuống theo phương thẳng đứng.

Phương trình sóng

Phương trình sóng tại một điểm

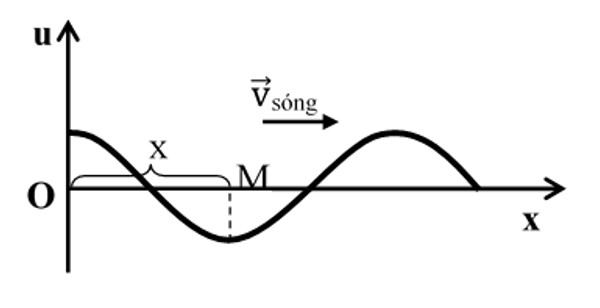
Sóng phát ra từ O (gốc tọa độ), với phương trình dao động: u_O = A_Ocos(ωt + φ). Điểm M cách O một khoảng bằng x, sóng truyền từ O đến M sẽ mất một khoảng thời gian là:

∆t = \frac{x}{v}

Phương trình dao động của M:

\begin{aligned}
&u_M=A_Mcos[ω(t-∆t)+φ]=A_Mcos\left[ω\left(t-\frac{x}{v}\right)+φ\right]\\
\Leftrightarrow\ &u_M=A_Mcos\left(ωt+φ-\frac{2\pi x}{λ}\right)\text{ với }ω=\frac{2\pi}{T} \text{ và }λ=v.T
\end{aligned}

Nếu bỏ qua năng lượng mất mát trong quá trình truyền sóng thì biên độ sóng tại O và biên độ sóng tại M sẽ bằng nhau: A_O = A_M = A

u_M=Acos\left[ω\left(t-\frac{x}{v}\right)+φ\right]=Acos\left(ωt+φ-\frac{2\pi x}{λ}\right)\text{ với }t\ge \frac{x}{v}

Sóng truyền theo chiều âm, từ trục Ox đến điểm N có tọa độ x sẽ có phương trình như sau:

u_N=Acos\left(ωt+φ+\frac{2\pi x}{λ}\right) \text{ với }t\ge \frac{|x|}{v}

Phương trình sóng tổng quát

Tại điểm O: u_O = Acos( ωt + j)

Tại điểm M cách O một đoạn bằng x trên phương truyền sóng.

• Nếu sóng cơ truyền theo chiều dương của trục Ox thì:

u_M=Acos\left(ωt+φ-\frac{2\pi x_M}{λ}\right) \text{ với }t\ge \frac{|x_M|}{v}

• Nếu sóng cơ truyền theo chiều âm của trục Ox thì:

u_M=Acos\left(ωt+φ+\frac{2\pi x_M}{λ}\right) \text{ với }t\ge \frac{|x_M|}{v}

Trong môi trường sóng cơ, tại một điểm M xác định: x = const thì u_M là hàm điều hòa theo t với chu kỳ T.

Ở một thời điểm xác định t = const thì u_M là hàm biến thiên điều hòa theo không gian x với chu kỳ λ.

Các điểm có cùng khoảng cách đến nguồn sóng dao động cùng pha.

\begin{aligned}&\small\text{Tại thời điểm }t < \frac{|x_M|}{v}, \text{ li độ dao động của điểm M luôn bằng 0 }(u_M = 0) \text{ vì sóng cơ chưa truyền}\\
&\small\text{đến điểm M.}
\end{aligned}

Độ lệch pha giữa 2 điểm được truyền đến từ cùng một nguồn

\begin{aligned}
&\small\bull\text{Phương trình dao động tại nguồn: }u = a.cos(ωt + φ).\\
&\small\bull\text{Phương trình dao động của nguồn truyền đến điểm }M_1: u_{1M} = a.cos\left(ωt + φ - \frac{2πd_1}{λ}\right)\\
&\small \text{ với }t ≥ \frac{d_1}{v}.\\
&\small\bull\text{Phương trình dao động của nguồn truyền đến điểm }M_2: u_{2M} = a.cos\left(ωt + φ - \frac{2πd_2}{λ}\right)\\
&\small \text{ với }t ≥ \frac{d_2}{v}.\\
&\small\bull\text{Độ lệch pha giữa điểm }M_1 \text{ và điểm }M_2: Δφ = \frac{2π}{λ}.(d_2 - d_1).\\
&\small\bull\text{Để hai dao động cùng pha thì: }Δφ = 2kπ \Rightarrow \frac{2π}{λ}.(d_2 - d_1) = 2kπ \Rightarrow d_2 - d_1 = kλ.\\
&\small\bull\text{Để hai dao động ngược pha thì: }Δφ = (2k+1)π\Rightarrow \frac{2π}{λ}.(d_2 - d_1) =(2k+1)π\\
&\small\Rightarrow d_2-d_1=(2k+1)\frac{λ}{2}\\
&\small\bull\text{Trên phương truyền sóng lệch pha nhau góc Δφ (rad), khoảng cách giữa hai điểm là: }\\
&\small L = \frac{Δφ}{2π}λ
\end{aligned}

Các em cần lưu ý các đơn vị tính cần phải tương ứng với nhau.

Tham khảo ngay các khoá học online của Marathon Education

Qua bài viết này, chắc chắn các em đã có thể tự mình trả lời được câu hỏi sóng cơ và sự truyền sóng cơ là gì rồi phải không? Mong rằng những thông tin này sẽ giúp các em nắm chắc hơn bài học trên lớp. 

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!