Lý thuyết và bài tập minh họa Chuyển động tròn đều
Chuyển động tròn đều là nội dung thường gặp trong các bài kiểm tra Vật lý. Vậy để hiểu rõ hơn về chuyển động tròn đều và cách giải các dạng bài tập về kiến thức này, các em hãy theo dõi bài viết sau của Team Marathon Education.
Xem thêm
- Vật Lý 10: Chuyển Động Thẳng Đều Lý Thuyết Và Bài Tập Minh Họa
- Tổng Hợp Công Thức Lý 10 Đầy Đủ, Dễ Nhớ
Chuyển động tròn và tốc độ trung bình trong chuyển động tròn

Chuyển động tròn được định nghĩa là chuyển động có quỹ đạo là một đường tròn.
Ví dụ: Chuyển động của một cabin trong trò chơi đu quay.
Công thức tính tốc độ trung bình trong chuyển động tròn:
v_{tb}=\frac{\Delta s}{\Delta t}
>>> Xem thêm: Lý Thuyết Lý 10: Chuyển Động Cơ Và Bài Tập Minh Họa
Chuyển động tròn đều là gì?

Chuyển động tròn đều được định nghĩa là chuyển động có quỹ đạo tròn và tốc độ trung bình trên mọi cung tròn là như nhau.
Ví dụ: Chuyển động đều của đầu kim giờ trong đồng hồ.
>>> Xem thêm: Lý Thuyết Lý 10: Chuyển Động Thẳng Biến Đổi Đều
Các đại lượng trong chuyển động tròn đều
Tốc độ dài (Vận tốc)
Tốc độ dài trong chuyển động tròn đều
Gọi Δs là độ dài cung tròn mà vật di chuyển được trong khoảng thời gian rất ngắn. Ta có công thức tính tốc độ dài của vật là:
v=\frac{\Delta s}{\Delta t}
Trong chuyển động tròn đều tốc độ dài của vật có độ lớn luôn không đổi.
>>> Xem thêm: Thế Năng Là Gì? Công Thức Tính Thế Năng Trọng Trường Và Thế Năng Đàn Hồi
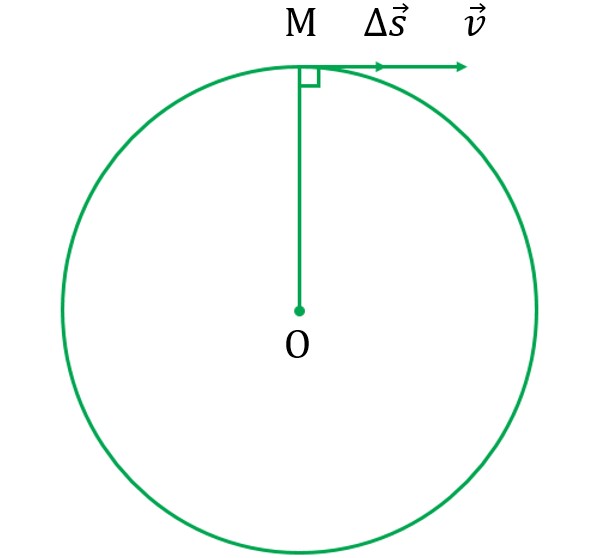
Vectơ vận tốc trong chuyển động tròn đều
\begin{aligned}
&\small\text{Xét một cung tròn có độ dài rất nhỏ (có thể xem như là một đoạn thẳng) có vectơ }\Delta\vec{s} \text{ để chỉ quãng }\\
&\small\text{đường đi được và chỉ hướng chuyển động. } \Delta\vec{s} \text{ được gọi là vectơ độ dời.}\\
&\small\text{Vì } \Delta\vec{s} \text{ phương với tiếp tuyến với đường tròn quỹ đạo tại M, }\Delta\vec{v} \text{ và }\Delta\vec{s} \text{ cùng phương với nhau nên }\vec{v}\\
&\small\text{cũng nằm dọc theo tiếp tuyến tại M. Từ đó, ta có thể thấy được vectơ vận tốc }\vec{v} \text{ trong chuyển động}\\
&\small\text{tròn đều luôn có phương tiếp tuyến với đường tròn quỹ đạo.}
\end{aligned}
Công thức tính vận tốc trong chuyển động tròn đều:
\vec{v}=\frac{\Delta\vec{s}}{\Delta t}
Đối với chuyển động tròn đều, vecto vận tốc có phương luôn luôn thay đổi.
Tốc độ góc
Tốc độ góc của chuyển động tròn đều được định nghĩa là đại lượng đo bằng góc mà bán kính OM quét được trong một đơn vị thời gian và đây là đại lượng không đổi.
Công thức tính tốc độ góc:
ω=\frac{\Delta α}{\Delta t}
Trong đó:
- Δα là góc bán kính OM quét được (rad)
- Δt là thời gian bán kính OM quét (s)
- ω là tốc độ góc (rad/s)
Chu kỳ
Chu kì T là thời gian để vật di chuyển hết một vòng. Đơn vị đo là giây (s).
T=\frac{2\pi}{\omega}
Tần số
Tần số f là số vòng mà vật di chuyển được trong 1 giây. Đơn vị đo của f là vòng/s hoặc Hec (Hz).
f=\frac{1}{T}
Công thức liên hệ giữa tốc độ dài và tốc độ góc
v=\omega.r
Trong đó:
- v là tốc độ dài (m/s)
- ω là tốc độ góc (rad/s)
- r là bán kính (m)
>>> Xem thêm: Lý Thuyết Tính Tương Đối Của Chuyển Động Và Bài Tập Minh Họa
Gia tốc hướng tâm trong chuyển động tròn đều
Trong chuyển động tròn đều, vận tốc luôn duy trì ổn định nhưng hướng lại thay đổi. Vì vậy, chuyển động này sẽ sinh ra gia tốc. Gia tốc luôn hướng vào tâm của quỹ đạo nên được gọi là gia tốc hướng tâm.
Công thức tính gia tốc hướng tâm
a_{ht}=\frac{v^2}{r}=r\omega^2
Trong đó:
- aht là gia tốc hướng tâm (m/s2)
- v là tốc độ dài (m/s)
- ω là tốc độ góc (rad/s)
- r là bán kính (m)
Bài tập minh họa về chuyển động tròn đều
Bài tập 1: Một máy gia tốc chuyển động tròn đều trên quỹ đạo có r = 1m. Thời gian máy gia tốc quay hết 5 vòng là 5.10-7s. Hãy tính vận tốc, tốc độ góc và gia tốc hướng tâm của máy.
Hướng dẫn giải:
\begin{aligned}
&T=\frac{t}{N}=\frac{5.10^{-7}}{5}=10^{-7}s\\
&\omega=\frac{2\pi}{T}=2\pi.10^{7}\ rad/s\\
&v=r.\omega=2\pi.10^7\ m/s\\
&a_{ht}=\omega^2.r=4\pi^2.10^{14}\ m/s^2
\end{aligned}
Bài tập 2: Một xe bán tải nhỏ chuyển động đều có đường kính của bánh xe là 80cm. Tính tần số, tốc độ góc và chu kì của đầu van xe.
Hướng dẫn giải:
Vận tốc xe bằng tốc độ dài: v = 10 m/s
Tốc độ góc là: ω = v.r = 12.5 (rad/s)
Chu kì là: T = 2πω = 0.5 (s)
Tần số là: f = 1T = 2 (vòng/s)
Bài tập 3: Một con quay chuyển động tròn đều quanh một trục có tâm là O, với vận tốc là 300 vòng/phút.
- Tính chu kì, tốc độ góc.
- Tính tốc độ dài và gia tốc hướng tâm của một điểm trên đĩa cách tâm là 10cm (g = 10 m/s2).
Hướng dẫn giải:
\begin{aligned}
&f=300 \ vòng/phút=5 \ vòng/s\\
&1)\ \omega=2\pi f=10\pi\ rad/s\\
&T=\frac{1}{f}=0,2s\\
&2) \ v=r\omega=0,1.10\pi=3,14\ m/s\\
&a_{ht}=\frac{v^2}{r}=98,7\ m/s^2
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Hy vọng những chia sẻ của Team Marathon Education về lý thuyết chuyển động tròn đều và cách giải bài tập có thể giúp các em ôn luyện lại kiến thức phần này. Việc thường xuyên làm bài tập và ghi chú những nội dung quan trọng sẽ giúp các em học môn Lý tốt hơn.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






