Dao Động Điều Hòa Là Gì? Công Thức Và Bài Tập Dao Động Điều Hòa Lý 12
Dao động điều hòa là nội dung quan trọng trong chương trình Lý 12. Trong bài viết dưới đây, Marathon chia sẻ đến các em lý thuyết về khái niệm, phương trình, các đại lượng đặc trưng của dao động điều hòa và các dạng bài tập liên quan đến chủ đề này. Các em hãy theo dõi bài viết nhé.
>>> Xem thêm: Lý Thuyết Và Bài Tập Con Lắc Lò Xo Lý 12 Đầy Đủ Và Chi Tiết
Dao động cơ là gì? Dao động tuần hoàn là gì?
Dao động cơ là dao động mà vật chuyển động qua lại quanh một vị trí đặc biệt được gọi là vị trí cân bằng.
Dao động tuần hoàn là dao động mà trạng thái của vật được lặp lại như cũ sau những khoảng thời gian bằng nhau xác định.
>>> Xem thêm: Thế Năng Là Gì? Công Thức Tính Thế Năng Trọng Trường Và Thế Năng Đàn Hồi
Dao động điều hòa là gì?
Trong phần lý thuyết, ta sẽ tìm hiểu về khái niệm, phương trình, các đại lượng đặc trưng của dao động điều hoà.
Khái niệm dao động điều hòa
Dao động điều hòa là dao động tuần hoàn mà phương trình trạng thái được biểu diễn dưới dạng các hàm điều hoà (sin hoặc cosin). Thời gian vật thực hiện một dao động toàn phần là một chu kỳ T. Số dao động toàn phần vật thực hiện được trong 1s là tần số f.
Từ đó, ta có công thức sau:
T=\frac{1}{f}
Trong công thức này, dao động cơ chuyển động qua lại quanh một vị trí cân bằng, chẳng hạn như chuyển động đung đưa của chiếc lá, chuyển động của con lắc đồng hồ…
>>> Xem thêm: Con Lắc Đơn – Lý Thuyết, Công Thức Và Bài Tập Minh Họa
Phương trình dao động điều hòa
Khi một điểm bất kỳ P dao động điều hòa trên một đoạn thẳng từ P1 đến P2, ta luôn có thể coi điểm P đó là hình chiếu của một điểm M tương ứng chuyển động tròn đều với tốc độ góc ω, trên đường tròn có đường kính là đoạn thẳng P2P1.
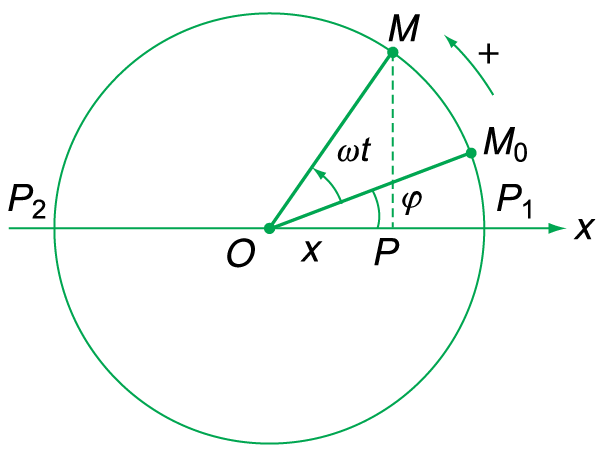
Giả sử t = 0, vật ở vị trí M0 được xác định bằng góc φ.
Tại thời điểm t, vị trí của M là (ωt + φ).
Khi đó hình chiều P của M có tọa độ x = A cos(ωt + φ).
Phương trình trên được gọi là phương trình của dao động điều hòa.
Với:
- x: Li độ của vật (đơn vị là m hoặc cm)
- A: Biên độ của vật (giá trị lớn nhất của li độ) (đơn vị là m hoặc cm)
- ω: Tốc độ góc trong chuyển động tròn đều (hoặc tần số góc trong dao động điều hòa) (đơn vị là rad/s)
- ωt + φ: Pha dao động tại thời điểm t
- φ: Pha ban đầu (pha dao động tại thời điểm ban đầu) (đơn vị là rad)
Các đại lượng đặc trưng của dao động điều hòa

Trong dao động điều hoà, các em cần nắm vững các đại lượng đặc trưng gồm chu kì, tần số dao động, tần số góc, vận tốc, gia tốc dao động điều hòa.
Chu kì
Chu kì là khoảng thời gian để vật thực hiện được một dao động toàn phần.
Đơn vị của chu kì là s (giây).
Tần số dao động
Tần số f là số dao động toàn phần thực hiện được trong một giây.
Đơn vị của tần số là Hz (héc)
Tần số góc
Tần số góc ω là đại lượng liên hệ với chu kì T hay với tần số f qua hệ thức dưới đây.
\omega=\frac{2\pi}{T}=2\pi f
- Đơn vị của tần số góc là rad/s.
- Một chu kì dao động vật đi được quãng đường là S = 4A.
- Chiều dài quỹ đạo chuyển động của vật là L = 2A.
Vận tốc dao động điều hòa
v = x' = -Aωsin(ωt + φ) = ωAcos(ωt + φ + \frac{π}{2})
\begin{aligned}
&\small\bull\text{Tại vị trí cân bằng (VTCB), vận tốc có độ lớn cực đại: }v_{max} = ωA\\
&\small\bull\text{Tại biên, vận tốc tốc bằng 0}\\
&\small\bull\text{Vận tốc nhanh pha hơn li độ một góc }\fracπ2 \text{ và vận tốc đổi chiều tại biên độ.}
\end{aligned}
Gia tốc
a = v' = x'' = -ω2A = -ω2Acos(ωt + φ) = ω2Acos(ωt+φ + π)
\begin{aligned}
&\small\bull\text{Vectơ gia tốc luôn luôn hướng về vị trí cân bằng.}\\
&\small\bull\text{Gia tốc có độ lớn tỉ lệ với độ lớn của li độ: }|a| ∼ |x|.\\
&\small\bull\text{Tại biên, gia tốc có độ lớn cực đại }a_{max} = ω2A.\\
&\small\bull\text{Tại VTCB, gia tốc bằng 0.}\\
&\small\bull\text{Gia tốc nhanh pha hơn vận tốc một góc }\fracπ2 \text{ và ngược pha so với li độ.}\\
\end{aligned}
>>> Xem thêm: Lý Thuyết Lý 10: Sự Rơi Tự Do Và Cách Giải Bài Tập Sự Rơi Tự Do
Mối quan hệ giữa li độ (x), vận tốc (v) và gia tốc (a)
\begin{aligned}
\small\bull\ &\text{Vận tốc v sớm pha hơn li độ x một góc }\frac{\pi}{2}:\\
&\small \left(\frac{x}{A} \right)^2+\left(\frac{v}{\omega A}\right)^2=1 \Leftrightarrow \begin{cases}A=\sqrt{x^2+\left(\frac{v}{\omega}^2 \right)}\\
x=\pm\sqrt{A+\left(\frac{v}{\omega}^2 \right)}\\
v=\pm \omega\sqrt{A^2-x^2}
\end{cases}\\
\small\bull\ &\text{Gia tốc a sớm pha hơn vận tốc v một góc }\frac{\pi}{2}:\\
&\left( \frac{a}{\omega^2 A}\right)^2+\left(\frac{v}{\omega A}\right)^2=1\\
\small\bull\ &\text{Gia tốc a và li độ x ngược pha:}\\
&a=-\omega^2x
\end{aligned}
Bài tập dao động điều hòa
Bài tập 1: Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Từ thời điểm vật qua vị trí có li độ 3,5 cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ hai, vật có tốc độ trung bình là bao nhiêu?
Lời giải:
\begin{aligned}
&\small\text{Quỹ đạo thẳng dài 14 cm nên biên độ }A=\frac{14}{2}=7\ cm\\
&\small\text{Gia tốc của vật đạt giá trị cực tiểu: } a_{min} = -A.ω^2\\
&\small\text{Khi đó: }x = +A = 7\ cm\\
&\small\text{Quãng đường vật đi được từ thời điểm vật đi qua vị trí có li độ 3,5 cm theo chiều dương đến khi gia}\\
&\small\text{tốc của vật đạt giá trị cực tiểu lần thứ hai là: } S = \frac{A}{2} + 4A = 31,5\ cm.\\
&\small\text{Khoảng thời gian tương ứng: } ∆t = \frac{T}{6} + T = \frac76s.\\
&\small\text{Tốc độ trung bình của vật trong khoảng thời gian này là: }v_{tb}=\frac{S}{\Delta t}=\frac{31,5}{\frac76}=27\ cm/s
\end{aligned}
Bài tập 2: Một vật nhỏ khối lượng 200 g dao động điều hòa với tần số 0,5 Hz. Khi lực kéo về tác dụng lên vật là 0,1 N thì động năng của vật có giá trị 1 mJ. Lấy π2 = 10. Tính tốc độ của vật khi đi qua vị trí cân bằng.
Lời giải:
\begin{aligned}
&a=\frac{F}{m}=0,5m/s^2\\
&v=\sqrt{\frac{2E_d}{m}}=0,1\ m/s\\
&v_{max}=\sqrt{\frac{a^2}{\omega^2}+v^2}=0,187\ m/s
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Trên đây là bài tổng hợp toàn bộ kiến thức về chủ đề dao động điều hòa và một số bài tập minh hoạt liên quan. Team Marathon Education hy vọng bài viết này sẽ giúp các em nắm vững lý thuyết cũng như biết cách vận dụng công thức để giải bài tập nhanh chóng. Các em hãy theo dõi website Marathon để học online trực tuyến nhiều kiến thức Toán – Lý – Hóa – Văn bổ ích khác. Chúc các em học hành tiến bộ và luôn đạt điểm cao!






