Lý thuyết và bài tập về các tập hợp số môn Toán học
Tập hợp số là khái niệm quen thuộc trong Toán học từ cấp THCS lên THPT. Hôm nay mời bạn cùng ôn tập kiến thức về các tập hợp số với Marathon Education qua bài viết dưới đây.

1. Tập hợp số là gì? Phần tử của tập hợp là gì?
- Tập hợp số là một khái niệm cơ bản trong toán học và không có một định nghĩa chung. Các tập hợp số được biểu diễn bằng các chữ cái in hoa như A, B, R, X, Y và các chữ thường như a, b, x, y, z đại diện cho phần tử trong tập hợp.
- Khi nói a∈A có nghĩa rằng a là một thành viên của tập hợp A; hoặc nói cách khác, a thuộc tập hợp A. Trái lại, ký hiệu aA biểu thị a không thuộc tập hợp A.
2. Các tập hợp số trong toán học cơ bản
2.1. Tập hợp các số tự nhiên (N)
Tập hợp các số tự nhiên được quy ước kí hiệu là N: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}.
>> Mời bạn xem thêm: Lý thuyết và bài tập tính giá trị của biểu thức môn Toán
2.2. Tập hợp các số nguyên (Z)
Tập hợp các số nguyên được quy ước kí hiệu là Z: Z={…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}. Đối với số nguyên dương, tập hợp sẽ được kí hiệu là N*.
2.3. Tập hợp các số hữu tỉ (Q)
Các tập hợp số số hữu tỉ được quy ước kí hiệu là Q: Q = {1,2; 2,3; 3,4;…}. Có thể diễn đạt số hữu tỉ bằng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn.
2.4. Tập hợp các số thực (R)
Tập hợp của các số thực được đặt ký hiệu là R. Khi một số thập phân vô hạn không tuần hoàn, ta xem đó là số vô tỉ và đặt nó trong tập hợp I. Tập hợp của số thực bao gồm cả số vô tỉ và số hữu tỉ (R=Q∪I).
2.5. Tập hợp rỗng
Tập hợp rỗng là tập hợp không chứa phần tử nào, ký hiệu là .
>> Dành cho bạn: Khái niệm và cách tính chu vi các hình môn Toán
3. Mối quan hệ của các tập hợp trong toán học
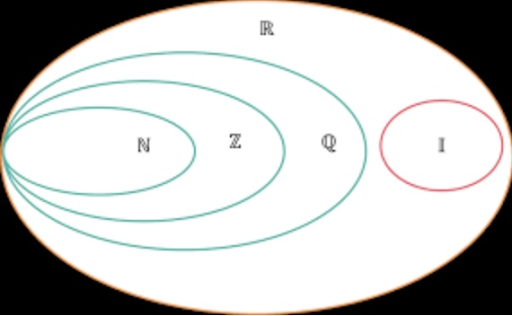
⇒ Quan hệ bao hàm giữa các tập hợp số là: N ⊂ Z ⊂ Q ⊂ R (minh họa trên hình).
4. Các phép toán trong tập hợp
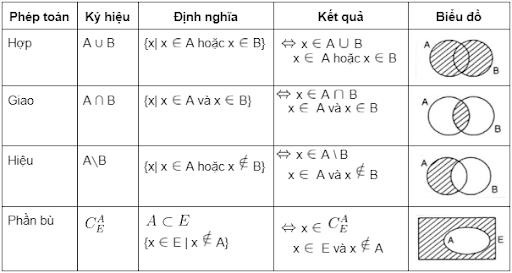
5. Bài tập
Bài tập 1:
a) Xác định tập hợp A là tập hợp của các số tự nhiên nhỏ hơn 10.
b) Xác định tập hợp B là tập hợp của các số chẵn nhỏ hơn hoặc bằng 10.
c) Xác định tập hợp C là tập hợp của các số lẻ dương nhỏ hơn 10.
Đáp án:
a) A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
b) B = {0, 2, 4, 6, 8, 10}
c) C = {1, 3, 5, 7, 9}
>> Công thức tính diện tích, chu vi hình tròn chính xác
Bài tập 2: Dựa vào các tập hợp đã nêu ở bài tập 1:
a) Tìm tập hợp hợp A ∪ B, tức là tập hợp gồm các số thuộc A hoặc B: A ∪ B = {x | x ∈ A hoặc x ∈ B}.
b) Tìm tập hợp A ∩ B, tức là tập hợp gồm các số thuộc cả A và B: A ∩ B = {x | x ∈ A và x ∈ B}.
c) Tìm tập hợp A \ B, tức là tập hợp gồm các số thuộc A nhưng không thuộc B: A \ B = {x | x ∈ A và x ∉ B}.
Đáp án:
a) A ∪ B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b) A ∩ B = {0, 2, 4, 6, 8}
c) A \ B = {1, 3, 5, 7, 9}

Bài tập 3: Cho tập hợp D = {3, 6, 9, 12, 15, 18}.
a) Xác định tập hợp E là tập hợp các số chia hết cho 3 trong tập D.
b) Xác định tập hợp F là tập hợp các số chẵn trong tập D.
Đáp án:
a) E = {3, 6, 9, 12, 15, 18}
b) F = {6, 12, 18}
Học Toán chưa lúc nào là dễ dàng! Tuy nhiên nếu cố gắng thì chắc chắn bạn sẽ thành công chinh phục môn Toán. Đừng quên ghé Marathon Education để xem thêm nhiều kiến thức bổ ích của môn Toán nhé!
Các Bài Viết Liên Quan






