Lý thuyết về hàm số liên tục | SGK Toán lớp 11

Trong chương trình Toán học lớp 11, các em sẽ được làm quen khái niệm về hàm số liên tục. Cùng nhiều dạng bài tập liên quan từ cơ bản đến nâng cao. Do vậy, để củng cố hơn phần kiến thức này, hãy cùng team Marathon Education tổng hợp đầy đủ lý thuyết và bài tập về hàm số liên tục. Các em có thể tham khảo làm tài liệu cho các kì kiểm tra sắp tới nhé!

Định nghĩa hàm số liên tục

Cho hàm số y= f(x) xác định trên khoảng K và x₀ ∈ K. Hàm số y= f(x) được gọi là hàm số liên tục tại x₀ nếu .

• Hàm số y= f(x) không liên tục tại x₀ hay còn gọi là gián đoạn tại điểm đó.
• Hàm số y= f(x) liên tục trên khoảng nếu hàm số đó liên tục tại mọi điểm thuộc khoảng đó.
• Hàm số y=f(x) liên tục trên đoạn [a;b] nếu nó liên tục trên khoảng (a;b) và

Đồ thị của hàm số liên tục trên một khoảng là một đường nối liền trên khoảng đó.

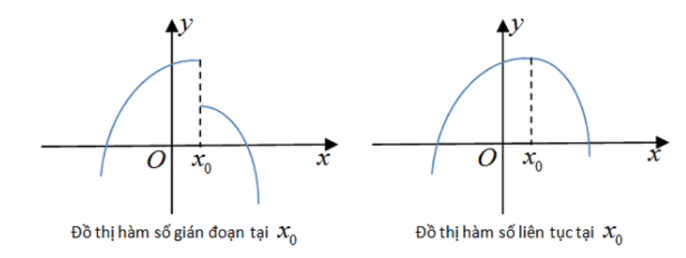
Những định lý cơ bản về hàm số liên tục

Định lý 1

• Hàm số đa thức liên tục trên toàn bộ tập hợp số thực R.
• Hàm số lượng giác và hàm số phân thức hữu tỉ (thương của hai đa thức) liên tục trên từng khoảng của tập xác định của chúng.

 

 

Định lý 2

Giả sử: Hàm số y= f(x) và y= g(x) là 2 hàm số liên tục tại x₀. Ta có:

• Các hàm số y= f(x) + g(x), y= f(x) – g(x) và y= f(x). g(x) liên tục tại x;
• Hàm số y = f(x)g(x) liên tục tại điểm x₀ nếu g(x₀) 0.

Định lý 3

Nếu hàm số y= f(x) liên tục trên đoạn [a;b] bất kì và f(a). f(b) < 0 thì hàm số sẽ tồn tại ít nhất một điểm c (a,b) sao cho f(c) = 0.

Định lý này được áp dụng để chứng minh sự tồn tại nghiệm của phương trình trên một khoảng và nó còn được phát triển dưới dạng khác như sau:

• Hàm số y= f(x) liên tục trên đoạn [a;b] và f(a). f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a;b)

Với những thông tin mà Marathon Education đã tổng hợp và chia sẻ ở trên, hy vọng các em có thể giải các bài tập hàm số liên tục. Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!

Tham khảo ngay các khoá học online của Marathon Education