Tích Vô Hướng Của Hai Vectơ: Lý Thuyết Và Giải Bài Tập

Để học toán hiệu quả, các em cần hiểu được lý thuyết thì mới có thể giải được bài tập nhanh chóng và có kết quả đúng. Đối với tích vô hướng của hai vectơ, các em hãy ôn luyện và áp dụng vào việc giải toán thông qua các công thức được Marathon Education cung cấp trong bài viết sau. 

Định nghĩa

Cho 2 vectơ và đều khác vectơ . Tích vô hướng của và có kí hiệu là ,và được xác định bởi công thức sau đây: 

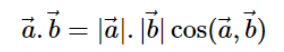
Chú ý: 

• Trong trường hợp có ít nhất 1 trong 2 vectơ và bằng vectơ ta có:
• Khi và khác vectơ ta có:
• Khi = sẽ có tích vô hướng là và được kí hiệu là . Số này được gọi là bình phương vô hướng của vectơ . Ta có:

Tính chất tích vô hướng của hai vectơ

Tích vô hướng của 2 vectơ có các tính chất sau đây: 

Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:

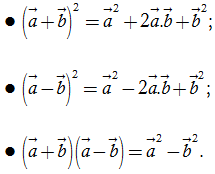
Biểu thức tọa độ của tích vô hướng

Trên mặt phẳng tọa độ , cho hai vectơ: Khi đó tích vô hướng của .là:

Nhận xét: Hai vectơđều khác vectơ vuông góc với nhau khi và chỉ khi: a₁b₁ + a₂b₂ = 0. 

 

 

Ứng dụng tích vô hướng

• Độ dài vectơ

Các em có thể tính độ dài của vectơ = (a₁, a₂) theo công thức như sau:

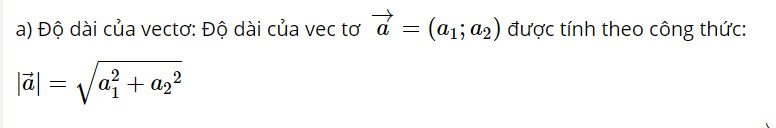
• Góc giữa 2 vectơ

Từ định nghĩa tích vô hướng của hai vectơ, chúng ta suy ra được nếu = (a₁, a₂) và = (b₁, b₂) đều khác thì ta có:

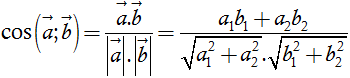
• Khoảng cách giữa hai điểm

Khoảng cách giữa hai điểm A(x_A; y_A) và B(x_B; y_B) được tính theo công thức sau:

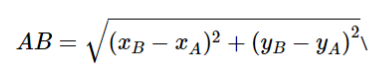
Tham khảo ngay các khoá học online của Marathon Education

 

 

 

 

Như vậy các em đã được tìm hiểu tổng hợp lý thuyết tích vô hướng của hai vectơ đầy đủ và rõ ràng qua bài viết trên. Để ứng dụng vào bài tập một cách hiệu quả, các em cần học thuộc các công thức từ tính chất đến cách tính độ dài, góc và khoảng cách. 

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!

>> Có thể bạn quan tâm:

• Tổng hợp các dạng hình học không gian thường gặp nhất
• Lý Thuyết Phương Trình Đường Tròn 10 Môn Toán
• Ma trận đề thi THPT quốc gia 2023 cập nhật các môn