Hàm Số Bậc Nhất – Lý Thuyết Và Phương Pháp Giải Bài Tập

Hàm số là một trong những lý thuyết quan trọng trong chương trình toán đại số. Có nhiều dạng bài tập xoay quanh chủ đề này liên quan đến các loại hàm số khác nhau. Hàm số bậc nhất là một dạng hàm số cơ bản nhất, khởi nguồn cho các kiến thức hàm số nâng cao hơn mà các em sẽ được học trong chương trình toán trung học. Bài viết này, Marathon Education sẽ giúp  các em có thể nắm vững các kiến thức cũng như phương pháp giải bài tập hàm số bậc nhất một cách đầy đủ nhất, chuẩn bị cho những kì thi sắp tới.

Hàm số bậc nhất

Khái niệm hàm số bậc nhất

Hàm số bậc nhất là hàm số có dạng: y = ax + b với a,b là các số cho trước và a ≠ 0

Khi b = 0 hàm số sẽ có dạng y = ax

Tính chất hàm số bậc nhất

Hàm số bậc nhất y = ax + b xác định với mọi x thuộc R, có tính chất như sau:

• Hàm số đồng biến trên R nếu a > 0
• Hàm số nghịch biến trên R nếu a < 0

 

Đồ thị hàm số bậc nhất

Lý thuyết hàm số bậc nhất và đồ thị

Đồ thị của hàm số bậc nhất y = ax + b là một đường thẳng, cắt trục tung tại điểm có tọa độ ( 0 ; b ), trùng với đường thẳng y = ax nếu b = 0 và song song với y = ax nếu b ≠ 0.

Khi đó: a được gọi là hệ số góc, b là tung độ góc của đường thẳng y = ax + b

Xem thêm: Bảng Nguyên Hàm Và Công Thức Nguyên Hàm Đầy Đủ, Chi Tiết

Cách vẽ đồ thị hàm số bậc nhất

• Xét trường hợp y = ax + b với a ≠ 0, b ≠0

Như đã biết, đồ thị hàm số bậc nhất là một đường thẳng, do vậy để vẽ được đồ thị này, về cơ bản ta chỉ cần xác định được 2 điểm thuộc đường thẳng y = ax + b là đã có thể vẽ được đồ thị.

• Trường hợp hàm số y = ax + b với b = 0

Khi b=0 thì y=a.x. Đồ thị của hàm số y= ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).

Xác định 2 điểm bất kì thuộc đường thẳng y = ax + b

Ví dụ:

Lấy điểm A có hoành độ x­₁, hoành độ y₁ = x + b ⇒ A ( x­₁ ; x­₁+b )

Lấy điểm B có hoành độ x₂, hoành độ y₂ =  x₂ + b ⇒ B (x₂ ; x₂ + b )

Sau đó, vẽ 1 đường thẳng đi qua 2 điểm A, B là ta đã có được đồ thị hàm số.

Chú ý: Khi lấy các tọa độ để vẽ đồ thị, các em nên lấy tọa độ chẵn để dễ chọn điểm trên trục tọa độ.

Các dạng bài tập đồ thị hàm số bậc nhất

Dưới đây là một số bài tập vận dụng về đồ thị hàm số bậc nhất, các em có thể tham khảo luyện tập.

Bài tập 1:

Vẽ đồ thị hàm số sau:

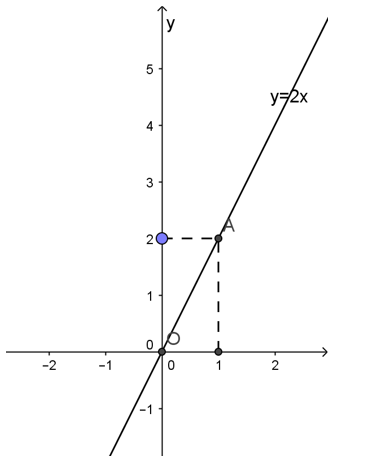
a/ y = 2x

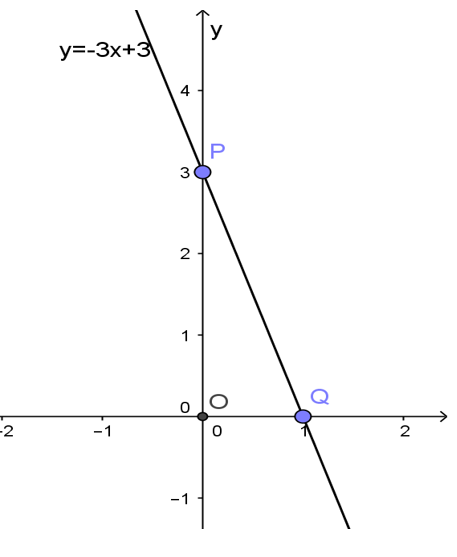
b/ y = -3x+3

Bài giải:

Ta có:

Đồ thị hàm số y = 2x đi qua điểm O(0; 0) và điểm A(1; 2)

Đồ thị của hàm số y = 2x có dạng:

b/ y = -3x+3

• Lấy x = 0 ⇒ y=3, ta được điểm A(0; 3) thuộc trục tung Oy
• Lấy y = 0 ⇒ x=1, ta được điểm B(1; 0) thuộc trục hoành Ox

Khi đó, vẽ đường thẳng đi qua hai điểm A, B ta đc đồ thị:

Bài tập 2:

Cho các hàm số sau:

1. y = 2mx + m + 1 
2. y = (m-1)x + 3

a/ Xác định m để hàm số (1)  đồng biến, hàm số (2) nghịch biến

b/ Xác định m để đồ thị hai hàm số song song

c/  Chứng minh: đồ thị của hàm số (1) luôn đi qua một điểm cố định với mọi giá trị m

Bài giải:

a/ 

• Hàm số (1) y = 2mx + m + 1 đồng biến khi a > 0 tức là 2m > 0 ⇒ m > 0
• Hàm số (2) y = (m-1)x + 3 nghịch biến khi a < 0 tức là m – 1 < 0 ⇔ m < 1

⇒ Để hàm số (1) đồng biến, hàm số (2) nghịch biến thì m phải thỏa mãn: 0 < m < 1

b/ Để đồ thị hai hàm số song song thì:

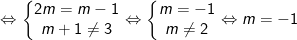
Như vậy, m = -1 thì đồ thị hàm số (1) song song đồ thị hàm số (2).

c/ Viết lại hàm số (1) ta được: y = m(2x+1) + 1

Với mọi giá trị m, khi x = -½ thì y = 1, do đó hàm số luôn đi qua 1 điểm có tọa độ (-½; 1) với mọi m.

Bài tập 3:

Cho hàm số y = (m-3)x + m + 2 (3)

a/ Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 3

b/ Tìm m để đồ thị hàm số song song với đường thẳng d₁: y = -2x + 1

c/ Tìm m để đồ thị hàm số vuông góc với đường thẳng d₂: y = 2x – 5

Bài giải:

a/ Để đồ thị hàm số (3) cắt trục tung tại điểm có tung độ bằng  -3 thì x = 0 và y = -3

Nên ta có: -3 = (m-3).0 + m + 2 ⇔ m = -5

Suy ra, khi m = -5 thì đồ thị hàm số (3) cắt trục tung tại điểm có tung độ bằng -3

b/

Gọi:

a’ là hệ số góc của d₁

b’ là tung độ góc của d₁

Để đồ thị hàm số y = (m-3)x + m + 2 song song với đường thẳng d₁: y = -2x + 1 thì

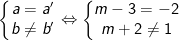
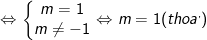
Vậy m = 1 thì đồ thị hàm số song song với đường thẳng d₁

c/ Để đồ thị hàm số y = (m-3)x + m + 2 vuông góc với đường thẳng d₂ thì:

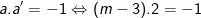
Suy ra, khi m = 5/2 thì đồ thị hàm số (3) vuông góc với đường thẳng d₂

Trên đây là những lý thuyết cơ bản về hàm số bậc nhất cùng một số bài tập vận dụng liên quan giúp các em nắm chắc hơn kiến thức của chủ đề này. Để giỏi toán, các em cần nắm vững kiến thức và làm thật nhiều bài tập, do vậy, đừng quên đăng ký học online cùng với Marathon Education để ôn luyện nhiều hơn, đạt được điểm số cao hơn trong học kỳ sắp tới.

Tham khảo ngay các khoá học online của Marathon Education