Bảng Nguyên Hàm Và Công Thức Nguyên Hàm Đầy Đủ, Chi Tiết
Nguyên hàm là một trong những chuyên đề quan trọng của Giải tích Toán 12 và thường xuất hiện nhiều trong các kì thi đại học. Vậy có những công thức nguyên hàm quan trọng nào cần nhớ? Team Marathon Education sẽ giúp các em giải đáp và tìm hiểu rõ hơn về bảng công thức nguyên hàm từ cơ bản đến nâng cao và phương pháp giải bài tập nguyên hàm phổ biến qua bài viết dưới đây.
>>> Xem thêm: Toán 12 Nguyên Hàm – Lý Thuyết Và Hướng Dẫn Giải Bài Tập
Nguyên hàm là gì?
Trước khi, đi sâu vào tìm hiểu công thức về nguyên hàm, các em cần nắm vững khái niệm nguyên hàm cũng như các tính chất và định lý liên quan.
Định nghĩa nguyên hàm
Cho hàm số f(x) xác định trên K, lúc này hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) (với mọi x ∊ K, K có thể là khoảng, đoạn hoặc nửa đoạn trên ℝ).
Kí hiệu nguyên hàm của hàm số f(x) là:
\int f(x)dx=F(x)+C \ \ \ (\forall \ C\in\R)
Định lý nguyên hàm
3 định lý của nguyên hàm là:
- Định lý 1: Giả sử F(x) là một nguyên hàm của f(x) trên K. Khi đó, với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x).
- Định lý 2: Trên K, nếu F(x) là một nguyên hàm của hàm số f(x) thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số tùy ý.
- Định lý 3: Trên K, tất cả hàm số f(x) liên tục đều có nguyên hàm.
Tính chất nguyên hàm
3 tính chất cơ bản của nguyên hàm được thể hiện như sau:
\begin{aligned}
&\footnotesize\bull\text{Nếu f(x) là hàm số có nguyên hàm thi: }(\smallint f(x)dx)'=f(x)\ \text{và }\\
&\footnotesize\smallint f'(x)dx=f(x) +C.\\
&\footnotesize\bull\text{Nếu F(x) có đạo hàm thì }\smallint d(F(x))=F(x)+C.\\
&\footnotesize\bull\text{Tích của nguyên hàm với k là hằng số khác 0: }\smallint kf(x)dx=k\smallint f(x)dx.\\
&\footnotesize\bull\text{Tổng, hiệu của nguyên hàm: }\smallint [f(x)\pm g(x)]=\smallint f(x)dx\pm \smallint g(x)dx
\end{aligned}
Bảng công thức nguyên hàm cơ bản, mở rộng và nâng cao
Mỗi dạng nguyên hàm đều có những công thức riêng. Những công thức này đã được tổng hợp thành các bảng dưới đây để các em dễ dàng phân loại, ghi nhớ và áp dụng chính xác.
Bảng công thức nguyên hàm cơ bản

Bảng công thức nguyên hàm mở rộng
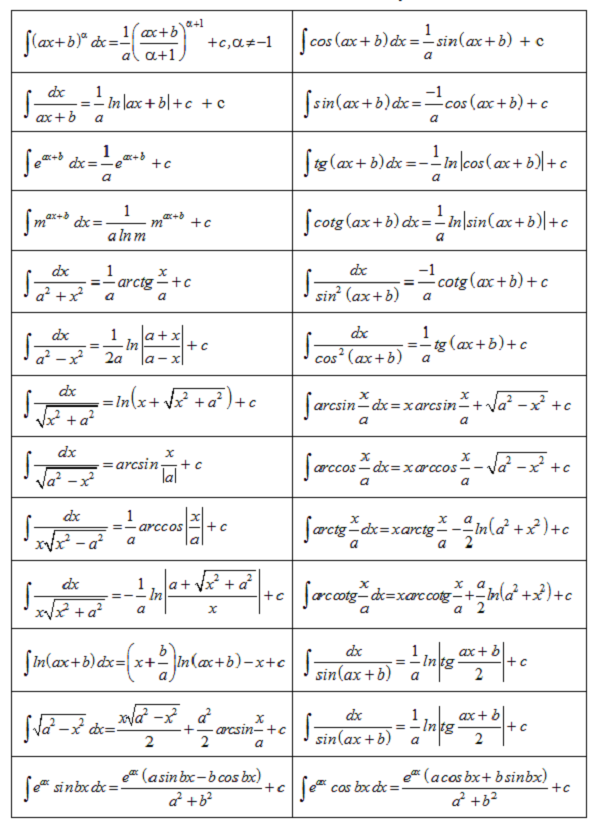
Bảng công thức nguyên hàm nâng cao

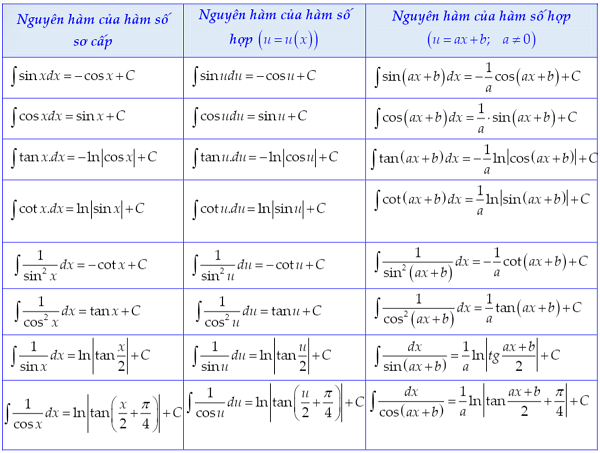
Bảng nguyên hàm hàm số lượng giác
2 phương pháp giải bài tập nguyên hàm phổ biến
Phương pháp đổi biến số
Đây là phương pháp được sử dụng rất nhiều khi giải nguyên hàm. Vì vậy, các em cần phải nắm vững phương pháp này để giải các bài toán nguyên hàm nhanh và chính xác hơn.
Phương pháp đổi biến loại 1:
Cho hàm số u = u(x) có đạo hàm liên tục trên K, y = f(u) liên tục để f[u(x)] xác định trên K và ∫f(u)du = F(u) + C thì:
∫f[u(x)]u'(x)dx = F[u(x)] + C
Cách giải:
Đầu tiên, chọn t = φ(x) và tính vi phân hai vế: dt = φ'(t)dt.
Sau đó, biến đổi biểu thức thành: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Kết quả: I = ∫f(x)dx = ∫g(t)dt = G(t) + C.
Phương pháp đổi biến loại 2: Khi đề bài cho hàm số f(x) liên tục trên K và x = φ(t) là một hàm số xác định, liên tục trên K và có đạo hàm là φ'(t). Lúc này:
∫f(x)dx = ∫f[φ(t)].φ'(t)dt
Cách giải:
Đầu tiên, chọn x = φ(t) và lấy vi phân hai vế: dx = φ'(t)dt.
Thực hiện biến đổi: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Tính: ∫f(x)dx = ∫g(t)dt = G(t) + C.
Phương pháp nguyên hàm từng phần
Phương pháp chung
Định lý: Nếu hai hàm số u(x) và v(x) có đạo hàm liên tục trên K thì:
\small \smallint u(x)v'(x)dx=u(x)v(x)-\smallint v(x)u'(x)dx\ \text{hay} \ \smallint udv=uv-\smallint vdu\\ (\text{với }du=u'(x)dx, \ dv=v'(x)dx)
Cách giải:
Trước hết, các em cần biến đổi tích phân đầu tiên về dạng:
I=\int f(x)dx=\int f_1(x)f_2(x)dx
Tiếp theo, đặt:
\begin{cases}u=f_1(x)\\dv=f_2(x)\end{cases}
\implies \begin{cases}du=f'_1(x)dx\\v=\int f_2(x)dx\end{cases}
Lúc này thì các em sẽ có:
\smallint udv=uv-\smallint vdu
Tùy thuộc vào từng dạng toán cụ thể mà các em áp dụng phương pháp sao cho phù hợp.
Các dạng nguyên hàm từng phần thường gặp
Dạng 1:
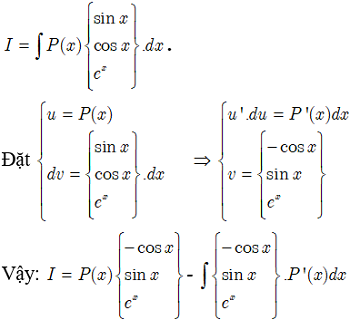
Dạng 2:
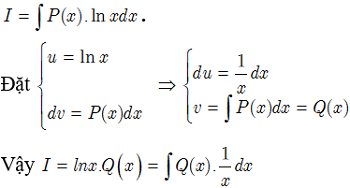
Dạng 3:
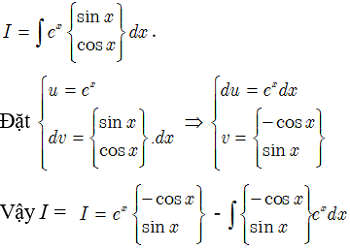
>>> Xem thêm: Phương Pháp Nguyên Hàm Từng Phần Và Công Thức Tính Chi Tiết Nhất
Bài tập về công thức nguyên hàm
Bài 1 Trang 126 SGK Toán 12
Đề bài:
a. Hãy nêu định nghĩa nguyên hàm của hàm số cho trước f(x) trên một khoảng.
b. Phương pháp tính nguyên hàm từng phần là gì? Đưa ra ví dụ minh họa cho cách tính đã nêu.
Hướng dẫn giải bài tập:
a. Xét hàm số y = f(x) xác định trên tập xác định D.
Hàm số Y = F(x) được gọi là nguyên hàm của hàm số y = f(x) trên D khi Y = F(x) thỏa mãn điều kiện F'(x) = f(x) ∀ x ∈ D.
b.
Phương pháp tính nguyên hàm từng phần được định nghĩa như sau:
Cho 2 hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên D, khi đó ta có công thức:
∫u(x).v’(x)dx = u(x).v(x) – ∫v(x).u’(x)dx hay ∫udv = uv – ∫vdv
Ví dụ minh họa: Tính nguyên hàm của hàm số A = ∫xexdx
Lời giải:
\begin{aligned}
& \small \text{Đặt }
\begin{cases}
u=x
\\
dv=e^xdx
\end{cases}
\implies
\begin{cases}
du=dx
\\
v=e^x
\end{cases}
\\
& \small \text{Khi đó, } A = \smallint xe^xdx = xe^x - \smallint e^xdx = xe^x - e^x + C
\end{aligned}
Bài 2 Trang 126 SGK Toán 12
Đề bài:
a. Nêu định nghĩa tích phân hàm số f(x) trên đoạn [a;b]
b. Tính chất của tích phân là gì? Nêu ví dụ cụ thể.
Hướng dẫn giải bài tập:
a. Xét hàm số y = f(x) liên tục trên [a; b], gọi F(x) là nguyên hàm của f(x) trên [a;b]
Khi đó, tích phân cần tìm là hiệu F(b)-F(a), kí hiệu:
I = \intop_a^bf(x)dx=F(b)-F(a)
b. Tính chất của tích phân:
\begin{aligned}
&\intop^a_bf(x)dx=0\\
&\intop^b_af(x)dx=-\intop^a_bf(x)dx\\
&\intop^b_akf(x)dx=k\intop^b_af(x)dx\\
&\intop^b_a{[f(x)\pm g(x)]}dx = \intop^b_a{f(x)dx}\pm \intop^b_a{g(x)dx}\\
&\intop^b_af(x)dx=\intop^c_af(x)dx+\intop^b_cf(x)dx
\end{aligned}
Bài 3 Trang 126 SGK Toán 12
Đề bài:
Tìm nguyên hàm của các hàm số đã cho dưới đây:
\begin{aligned}
&a. f(x)=(x-1)(1-2x)(1-3x)\\
&b. f(x)=sin(4x).cos^2(2x)\\
&c. f(x)=\frac{1}{1-x^2}\\
&d. f(x)=(e^x-1)^3
\end{aligned}
Hướng dẫn giải bài tập:
a. Ta có:
(x-1)(1-2x)(1-3x) = 6x^3 - 11x^2 + 6x - 1
Suy ra
\begin{aligned}
\small\int(x-1)(1-2x)(1-3x)dx&\small=\int(6x^3-11x^2+6x-1)dx\\
&\small =\frac{3}{2}x^4-\frac{11}{3}x^3+3x^2-x+C
\end{aligned}
b. Ta có:
\begin{aligned}
\small sin(4x).cos^2(2x)&=\frac{1}{2}sin4x.cos4x+\frac{1}{2}sin4x\\&=\frac{1}{8}sin8x+\frac{1}{2}sin4x
\end{aligned}
Suy ra:
\small \int(\frac{1}{8}sin8x+\frac{1}{2}sin4x)dx=-\frac{cos8x}{32}-\frac{cos4x}{8}+C
c. Ta có:
\begin{aligned}
\small f(x)&=\small \frac{1}{1-x^2}\\
&=\small \frac{1}{(1-x)(1+x)}\\
&=\small \frac{1}{2}.\frac{1+x+1-x}{(1-x)(1+x)}\\
&=\small \frac{1}{2}.\frac{1}{1-x}+\frac{1}{2}.\frac{1}{1+x}
\end{aligned}
Suy ra:
\begin{aligned}
\int f(x)dx&=\frac{1}{2}.\frac{1}{1-x}+\frac{1}{2}.\frac{1}{1+x} \\
&=\frac{1}{2}(ln|1+x|+ln|1-x|)+C\\
&=\frac{1}{2}ln\big|(1+x)(1-x)\big|+C\
\end{aligned}
d. Với bài tập này, các em có thể làm theo cách giải thông thường là khai triển hằng đẳng thức bậc 3 rồi áp dụng tính nguyên hàm cho từng hàm nhỏ. Hoặc các em còn có thể sử dụng cách đặt ẩn phụ để giải tìm nguyên hàm như sau:
Đặt\ t=e^x \implies dt=e^x.dx=t.dx \implies \frac{dt}{t}=dx
Ta có:
\begin{aligned}
\int f(x)dx&=\int(e^x-1)^3dx\\
&=\int \frac{(t-1)^3}{t}dt\\
&=\int \left(t^2-3t+3-\frac{1}{t}\right)dt\\
&=\frac{1}{3}t^3-\frac{3}{2}t^2+3t-ln|t|+C\\
&=\frac{1}{3}e^{3x}-\frac{3}{2}e^{2x}+3e^x-ln|e^x|+C\\
&=\frac{1}{3}e^{3x}-\frac{3}{2}e^{2x}+3e^x-x+C'\\
&(Với\ C' = C-1)
\end{aligned}
Bài 4 Trang 126 SGK Toán 12
Đề bài:
Tính một số nguyên hàm sau:
\begin{aligned}
&a)\int(2-x).sinxdx\\
&b) \int\frac{(x+1)^2}{\sqrt{x}}dx\\
&c) \int\frac{e^{3x}+1}{e^x+1}dx\\
&d)\int\frac{1}{(sinx+cosx)^2}dx\\
&e)\int\frac{1}{\sqrt{1+x}+\sqrt{x}}dx\\
&f)\int\frac{1}{(1+x)(2-x)dx}
\end{aligned}
Hướng dẫn giải bài tập:
\begin{aligned}
&\text{a) Đặt} \begin{cases}u=2-x\\dv=sinxdx\end{cases} \implies \begin{cases}du=-dx\\v=-cosx\end{cases}\\
&\text{Theo công thức tính tích phân từng phần:}\\
&\int(2-x)sinxdx\\
&=(2-x)(-cosx)-\int cosxdx\\
&=(x-2)cosx-sinx +C\\
&b) \int\frac{(x+1)^2}{\sqrt{x}}dx\\
&=\int\frac{(x^2+2x+1}{\sqrt{x}}dx\\
&=\int (x^\frac{3}{2}+2x^\frac{1}{2}+x^\frac{-1}{2})dx\\
&=\frac{2}{5}x^\frac{5}{2}+2.\frac{2}{3}x^\frac{3}{2}+2.x^\frac{1}{2}+C\\
&=\sqrt{x}(\frac{2}{5}x^2+\frac{4}{3}x+2)+C\\
&c)\int\frac{e^{3x}+1}{e^x+1}dx\\
&=\int\frac{(e^x+1)(e^{2x}-e^x+1)}{e^x+1}\\
&=\int (e^{2x}-e^x+1)dx\\
&=\frac{1}{2}e^{2x}-e^x+x +C\\
&d)\int\frac{1}{(sinx+cosx)^2}dx\\
&=\int\frac{1}{[\sqrt{2}.cos(x-\frac{\pi}{4})]^2}dx\\
&=\int\frac{1}{2.cos^2(x-\frac{\pi}{4})}dx\\
&=\frac{1}{2}.tan(x-\frac{\pi}{4})+C\\
&e) \int\frac{1}{\sqrt{1+x} +\sqrt{x}}dx\\
&=\int\frac{(x+1)-x}{\sqrt{x+1} +\sqrt{x}}dx\\
&=\int\frac{(\sqrt{x+1} -\sqrt{x})(\sqrt{x+1} +\sqrt{x})}{\sqrt{x+1} +\sqrt{x}}dx\\
&=\int(\sqrt{x+1} -\sqrt{x})dx\\
&=\frac{2}{3}(x+1)^\frac{3}{2}-\frac{2}{3}x^\frac{3}{2} +C\\
&=\frac{2}{3}(x+1)\sqrt{x+1}-\frac{2}{3}x\sqrt{x}+C\\
&g)\int\frac{1}{(1+x)(2-x)}dx\\
&=\int\frac{1+x+2-x}{3(1+x)(2-x)}dx\\
&=\int\frac{1+x}{3(1+x)(2-x)}dx+\int\frac{2-x}{3(1+x)(2-x)}dx\\
&=\frac{1}{3}\int\frac{1}{2-x}dx+\frac{1}{3}\int\frac{1}{1+x}dx\\
&=-\frac{1}{3}ln|2-x|+\frac{1}{3}ln|1+x|+C\\
&=\frac{1}{3}ln\big |\frac{1+x}{2-x}\big|+C
\end{aligned}
Đề THPT Chuyên KHTN Lần 4
Đề bài:
Cho các số nguyên a và b thỏa mãn
\begin{aligned}
& \small \intop_2^1 (2x+1)lnxdx = a +\frac32 + lnb
\end{aligned}
Hãy tính tổng P = a + b
Hướng dẫn giải bài tập:
\begin{aligned}
& \small \text{Đặt }
\begin{cases}
u=lnx
\\
dv=(2x+1)dx
\end{cases}
\implies
\begin{cases}
du=\frac1xdx
\\
v=x^2 +x
\end{cases}
\\
& \small \text{Khi đó, }
\\
& \small \intop_2^1 (2x+1)lnxdx
\\
& \small = (x^2 + x)lnx \left. \right|^2_1 - \intop_2^1 (x^2 + x).\frac1xdx
\\
& \small = 6ln2 - \intop_2^1 (x + 1)dx
\\
& \small = 6ln2 - \left.\left( \frac{x^2}{2} + x \right) \right|^2_1
\\
& \small = 6ln2 - (4 - \frac32)
\\
& \small = -4 + \frac32 + ln64
\\
& \small \text{Vậy a = -4 và b = 64. Lúc đó. P = a + b = 60.}
\end{aligned}
Đề thi thử Sở Giáo Dục Bình Thuận
Đề bài:
Cho hàm số F(x) là nguyên hàm của hàm số f(x). Khi biết F(3) = 3, hãy tính tích phân:
K = \intop_0^3 xf(x)dx
Hướng dẫn giải bài tập:
Đối với dạng bài nâng cao này, các em sẽ kết hợp 2 phương pháp là tích phân hàm ẩn (đặt ẩn phụ) và tích phân từng phần.
\begin{aligned}
& \small \text{Đặt n = x + 1, khi đó: }
\\
& \small K = \intop_0^3 xf(x)dx
\\
& \small = \intop_{-1}^2 F(x+1)d(x+1)
\\
& \small = \intop_3^0 F(n)dn
\\
& \small =1
\\
& \small \text{Kế tiếp, ta đặt }
\begin{cases}
u=x
\\
dv=f(x)dx
\end{cases}
\implies
\begin{cases}
du=dx
\\
v=F(x)
\end{cases}
\\
& \small \text{Lúc đó: }
\\
& \small K = \intop_0^1xf(x)dx = \left.xF(x)\right|_0^3 - \intop_0^3F(x)dx = 3F(3) - 1 = 8
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Qua bài viết trên, Team Marathon Education đã chia sẻ đến các em lý thuyết cơ bản về nguyên hàm, bàng nguyên hàm cơ bản và mở rộng và các công thức nguyên hàm cần nắm vững. Hy vọng bài viết sẽ giúp các em ghi nhỡ những công thức nguyên hàm này một cách hiệu quả và giúp vận dụng chúng để giải bài tập một cách nhanh chóng.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






