Trong bài viết này, Team Marathon Education đã hệ thống lại cho các em nội dung Toán 10 dấu của nhị thức bậc nhất. Với những kiến thức này, các em sẽ nắm vững được các định và khái niệm liên quan đến nhị thức bậc nhất bao gồm cách xét dấu và cách áp dụng dấu của nhị thức bậc nhất để giải các bài toán bất phương trình. Các em hãy cùng theo dõi bài viết sau.
>>> Xem thêm: Lý Thuyết Toán 10 Dấu Của Tam Thức Bậc Hai Và Cách Xét Dấu
>>> Xem thêm: Học Toán lớp 10 Online Hiệu Quả Cùng Marathon Education
Nhị thức bậc nhất với ẩn x có dạng f(x) = ax + b. Trong đó, a và b là 2 số bất kỳ đã cho trước, a ≠ 0.
>>> Xem thêm: Tổng Hợp Các Kí Hiệu Trong Toán Học Phổ Biến Đầy Đủ Và Chi Tiết
\begin{aligned}
&\small \text{Nhị thức }f(x)=ax+b\ (a≠0) \text{ cùng dấu với hệ số a khi x có các giá trị trong khoảng } \left(-\frac{b}{a}; +∞ \right) \\
&\small \text{và trái dấu với hệ số a khi x có các giá trị trong khoảng} \left(-∞;-\frac{b}{a}\right).\\
&\small\text{Bảng xét dấu của nhị thức bậc nhất }f(x) = ax + b \text{ như sau:}
\end{aligned}
Giả sử f(x) là một tích (hoặc thương) của các nhị thức bậc nhất. Ta xét dấu f(x) theo các bước sau:
Các em giải phương trình chứa ẩn ở mẫu theo 2 bước sau:
Ví dụ:
Giải phương trình:
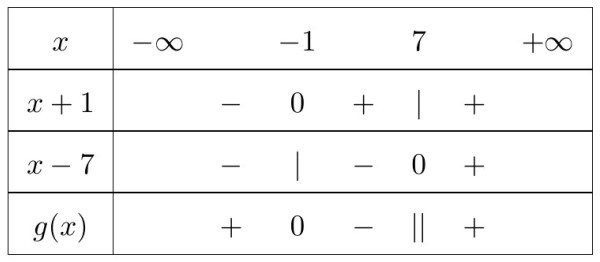
f(x) = \frac{x+1}{x-7}Bài giải:
f(x) không xác định khi x = 7
f(x) = 0 ⇔ x = -1
Bảng xét dấu:
Các em giải bất phương trình dạng tích theo 3 bước sau:
Ví dụ:
Giải bất phương trình:
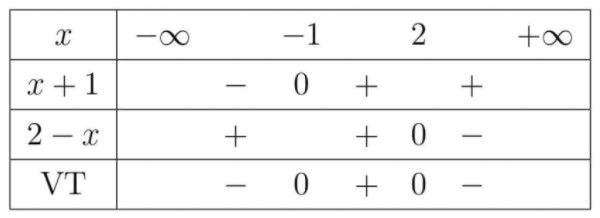
(x+2)(2-x) > 0
Bài giải:
Ta có:
x + 1 = 0 ⇔ x = -1\\ 2 - x = 0 ⇔ x = 2
Bảng xét dấu:
Bằng cách áp dụng tính chất của giá trị tuyệt đối các em có thể dễ dàng giải các bất phương trình dạng: |f(x)| ≤ a và |f(x)| ≥ a với a > 0 đã cho.
Với a > 0 ta có:
Ví dụ:
Giải bất phương trình:
|5x-4| ≥ 6
Bài giải:
Ta có:
|5x-4| ≥ 6 ⇔\left[\begin{array}{c}5x-4\geq 6\\5x-4\leq-6\end{array}\right.⇔\left[\begin{array}{c}x\geq2\\x\leq -\frac{2}{5}\end{array}\right.Kết luận:
S=\left(-∞;-\frac{2}{5}\right]\ ∪\ [2;+∞)>>> Xem thêm: Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10
Marathon Education là nền tảng học livestream trực tuyến Toán - Lý - Hóa - Văn - Anh - Sinh uy tín và chất lượng hàng đầu Việt Nam dành cho học sinh từ lớp 8 đến lớp 12. Với nội dung chương trình giảng dạy bám sát chương trình của Bộ Giáo dục và Đào tạo, Marathon Education sẽ giúp các em lấy lại căn bản, bứt phá điểm số và nâng cao thành tích học tập.
Tại Marathon, các em sẽ được giảng dạy bởi các thầy cô thuộc TOP 1% giáo viên dạy giỏi toàn quốc. Các thầy cô đều có học vị từ Thạc Sĩ trở lên với hơn 10 năm kinh nghiệm giảng dạy và có nhiều thành tích xuất sắc trong giáo dục. Bằng phương pháp dạy sáng tạo, gần gũi, các thầy cô sẽ giúp các em tiếp thu kiến thức một cách nhanh chóng và dễ dàng.
Marathon Education còn có đội ngũ cố vấn học tập chuyên môn luôn theo sát quá trình học tập của các em, hỗ trợ các em giải đáp mọi thắc mắc trong quá trình học tập và cá nhân hóa lộ trình học tập của mình.
Với ứng dụng tích hợp thông tin dữ liệu cùng nền tảng công nghệ, mỗi lớp học của Marathon Education luôn đảm bảo đường truyền ổn định chống giật/lag tối đa với chất lượng hình ảnh và âm thanh tốt nhất.
Nhờ nền tảng học livestream trực tuyến mô phỏng lớp học offline, các em có thể tương tác trực tiếp với giáo viên dễ dàng như khi học tại trường.
Khi trở thành học viên tại Marathon Education, các em còn nhận được các sổ tay Toán – Lý – Hóa “siêu xịn” tổng hợp toàn bộ công thức và nội dung môn học được biên soạn chi tiết, kỹ lưỡng và chỉn chu giúp các em học tập và ghi nhớ kiến thức dễ dàng hơn.
Marathon Education cam kết đầu ra 8+ hoặc ít nhất tăng 3 điểm cho học viên. Nếu không đạt điểm số như cam kết, Marathon sẽ hoàn trả các em 100% học phí. Các em hãy nhanh tay đăng ký học livestream trực tuyến Toán – Lý – Hóa – Văn lớp 8 – lớp 12 năm học 2022 – 2023 tại Marathon Education ngay hôm nay để được hưởng mức học phí siêu ưu đãi lên đến 39% giảm từ 699K chỉ còn 399K.
Trên đây là nội dung Toán 10 dấu của nhị thức bậc nhất. Các em nhớ dành thời gian xem kỹ lý thuyết và làm bài tập nhiều hơn để nắm vững kiến thức. Ngoài môn Toán, các em còn có thể tham khảo thêm nhiều kiến thức về lý thuyết và bài tập Lý – Hoá tại website Marathon Education. Chúc các em học ngày càng tiến bộ!
CÓ THỂ BẠN QUAN TÂM
