Lý thuyết Hoán vị, chỉnh hợp và tổ hợp lớp 10 bài 24
A. Lý thuyết
I. Hoán vị
- Định nghĩa
Cho một tập hợp A gồm n phần tử (n ∈ ℕ*).
Theo đó, mỗi một kết quả của việc sắp xếp thứ tự n phần tử của tập hợp A này gọi là một hoán vị của n phần tử đó.
Ví dụ: Từ 3 chữ số 2, 4, 6 có thể lập được bao nhiêu số có 3 chữ số hoàn toàn khác nhau?
Cách giải:
Dựa theo định nghĩa ta có: Mỗi một cách sắp xếp 3 chữ số đề bài đã cho để tạo thành một số có 3 chữ số hoàn toàn khác nhau là một hoán vị của 3 chữ số đó. Vậy ta có đáp án là:
246, 264, 426, 462, 624, 642
Vậy kết quả có 6 số có 3 chữ số khác nhau lập từ 3 chữ số 2, 4, 6
- Số các hoán vị
Các hoán vị của n phần tử được ký hiệu là Pn, cụ thể: Pn = n . (n – 1) … 2.1
Quy ước : Tích 1.2…n được viết là n! (đọc là n giai thừa), tức là n! = 1 . 2 … n.
Như vậy Pn = n!.
Ví dụ: Có ba học sinh Minh, Ngọc, Hà. Giáo viên muốn sắp xếp ba bạn học sinh này vào 3 vị trí chỗ ngồi. Vậy hỏi giáo viên có tất cả bao nhiêu cách sắp xếp?
Cách giải:
Xếp ba bạn Minh, Ngọc, Hà vào 3 vị trí chỗ ngồi là một hoán vị của 3 bạn học sinh này:
Ta có P3 = 3! = 1.2.3 = 6.
Vậy có tất cả 6 cách sắp xếp 3 bạn Minh, Ngọc, Hà vào 3 vị trí chỗ ngồi.
II. Chỉnh hợp
- Định nghĩa
Cho một tập hợp A gồm có n phần tử và một số nguyên k với 1 ≤ k ≤ n. Mỗi kết quả của việc lấy k phần tử từ n phần tử của tập hợp A và thực hiện sắp xếp chúng theo một trật tự nào đó thì gọi là chỉnh hợp chập k của n phần tử mà đề đã cho.
Ví dụ: Nhóm học sinh có 10 bạn, trong đó có 3 học sinh xuất sắc là: Dương, Hòa, Phương. Giáo viên muốn chọn 2 trong 3 bạn để làm nhóm trưởng và nhóm phó. Vậy hỏi giáo viên có tất cả bao nhiêu cách chọn?
Cách giải
Giáo viên có những cách sau để chọn 2 bạn trong nhóm này, một bạn làm nhóm trưởng và một bạn làm nhóm phó, cụ thể: Dương – Hòa, Hòa Dương, Dương – Phương, Phương – Dương, Phương – Hòa – Hòa Phương.
Tóm lại có 6 cách để giáo viên chọn ra 2 trong 3 bạn để đảm nhận vị trí nhóm trưởng và nhóm phó của nhóm học tập.
- Số cách chỉnh hợp
Kí hiệu 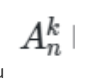 là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n).
là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n).
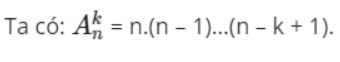
Ví dụ: Có 6 chữ số {3,4,5,6,7,8}. Hỏi 6 số trên có thể lập được bao nhiêu số có 3 chữ số đôi một khác nhau?
Cách giải:
Từ 6 chữ số đã cho, lấy 3 chữ số và sắp xếp để được một số có 3 chữ số khác nhau. Khi đó, các số tạo thành được gọi là chỉnh hợp chập 3 của 6 chữ số.
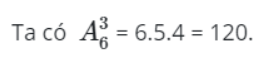
⇒ Có 120 số 3 chữ số được tạo thành
Vậy từ 6 chữ số đã cho bên trên trên, lập được 120 số có 3 chữ số đôi một khác nhau
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1
Đề bài:
Có 4 bạn An, Dung, Hồng, Cúc. Giáo viên muốn xếp 4 bạn này vào 4 tổ khác nhau. Hỏi giáo viên có tất cả bao nhiêu cách sắp xếp 4 bạn vào 4 tổ khác nhau.
Cách giải
Xếp 4 bạn An, Dung, Hồng, Cúc vào 4 tổ khác nhau là một hoán vị của 4 bạn đó.
Ta có P4 = 4! = 24.
⇒ Có 24 cách sắp xếp 4 bạn học sinh này vào 4 tổ khác nhau.
Vậy có 24 cách xếp 4 bạn An, Dung, Hồng, Cúc vào 4 tổ khác nhau.
Bài 2
Đề bài
Một nhóm có 7 học sinh. Giáo viên muốn chọn ra 3 bạn, trong đó một bạn học sinh đảm nhận làm nhóm trưởng và một bạn học sinh giữ vai trò làm nhóm phó, cuối cùng là một bạn học sinh làm thư ký. Vậy hỏi giáo viên có tất cả bao nhiêu cách chọn?
Cách giải
Theo yêu cầu của đề bài, mỗi cách chọn lần lượt 3 trong 7 bạn học sinh, trong đó một bạn làm nhóm trưởng, một bạn làm nhóm phó và một bạn làm thư ký. Thì đây là một chỉnh hợp chập 3 của 7 học sinh.
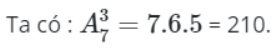
Vậy đáp án là có đến 210 cách chọn 3 trong 7 bạn để lần lượt giữ vai trò nhóm trưởng, nhóm phó và thư ký.
Bài 3
Đề bài
Bạn Hùng muốn đặt mật khẩu cho laptop. Theo đó, 4 kỳ tự đầu bạn sẽ lấy tên của mình, 3 ký tự sau là các chữ số. Hỏi Minh có tất cả bao nhiêu cách đặt mật khẩu cho laptop?
Cách giải:
4 ký tự đầu Minh lấy tên của mình nên có 1 cách chọn 4 ký tự đầu
3 ký tự sau là các con số, do đó ta sẽ có số cách chọn 3 trong 10 chữ số. Sau đó sắp xếp chúng là chỉnh hợp chập 3 của 10 chữ số.
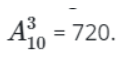
Theo quy tắc nhân ta có: 1 . 720 = 720. Vậy Hùng có đến 720 cách để đặt mật khẩu cho laptop của mình!
B.2 Bài tập trắc nghiệm
Câu 1. Sắp xếp ngẫu nhiên 3 bạn nam và 4 bạn nữ ngồi vào 7 chiếc ghế kê theo hàng ngang. Hỏi có tất cả bao nhiêu cách xếp sao cho 3 bạn nam ngồi cạnh nhau?
- A. 720
- B. 1 440
- C. 288
- D. 240
Cách giải
Đề bài yêu cầu 3 bạn nam xếp ngồi cạnh nhau, vì thế sẽ xem 3 bạn nam là 1 vị trí sắp xếp, còn lại 5 vị trí để xếp. Theo đó mỗi cách xếp 5 vị trí này chính là một hoán vị của 5 phần tử. Vậy tổng số cách xếp 5 vị trí là 5! = 120 (cách).
Ngoài 5 vị trí xếp trên trong nhóm 3 bạn nam ta cũng xếp 3 bạn vào 3 vị trí số cách xếp này là 3! = 12 (cách)
Áp dụng quy tắc nhân, ta có số cách xếp 3 bạn nam và 4 bạn nữ ngồi thành một hàng ngang đáp ứng điều kiện 3 bạn nam ngồi cạnh nhau là: 12.120 = 1 440 (cách).
Đáp án chính xác là đáp án B
Câu 2. Tìm số tự nhiên n thỏa
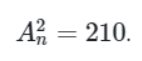
- A. 15
- B. 12
- C. 21
- D. 18
Cách giải
Điều kiện n ≥ 2; n ∈ ℕ
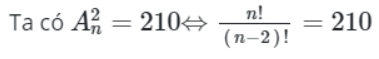
⇔ n(n – 1) = 210 ⇔ n2 – n – 210 = 0 ⇔ n = 15 hoặc n = –14
Kết hợp với điều kiện n = 15 thoả mãn
Đáp án chính xác là đáp án A
Câu 3. Trong một buổi liên hoan kỷ niệm ngày thành lập trường, cần chọn 4 tiết mục từ 6 tiết mục hát và 4 tiết mục từ 5 tiết mục múa, sau đó xếp thứ tự biểu diễn. Hỏi có tất cả bao nhiêu cách chọn và xếp thứ tự tiết mục sao cho thỏa mãn điều kiện các tiết mục hát và múa luôn xen kẽ nhau?
- A. 43 200
- B. 75
- C. 86400
- D. 480
Cách giải
Nếu đánh số theo tứ tự từ 1 – 8 cho các tiết mục biểu diễn, ta sẽ có 2 trường hợp:
Trường hợp 1: Tiết mục hát diễn ra đầu tiên
Trong trường hợp này, số lẻ là các tiết mục hát, số chẵn là các tiết mục múa. Thứ tự của những tiết mục múa và tiết mục hát được cố định, chỉ có thứ tự giữa các tiết mục múa hoặc giữa các tiết mục hát thay đổi.
Chọn 4 tiết mục hát từ 6 tiết mục hát và xếp thứ tự có:
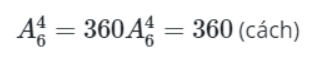
Chọn 4 tiết mục múa từ 5 tiết mục múa và xếp thứ tự có:
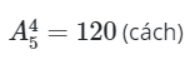
Vậy ta có số cách chọn và xếp thứ tự các tiết mục văn nghệ trong trường hợp tiết mục hát diễn ra đầu tiên là:
360.120 = 43. 200
Trường hợp 2: Tiết mục múa diễn ra đầu tiên
Nếu tiết mục múa diễn ra đầu tiên thì cách chọn và xếp thứ tự các tiết mục trong trường hợp này sẽ là:
120.360 = 43 200
Tóm lại, số cách chọn và xếp thứ tự các tiết mục văn nghệ sao cho các tiết mục hát và múa xen kẽ nhau sẽ được tính:
43 200 + 43 200 = 86 400.
Đáp án chính xác là đáp án C
>> Có thể bạn quan tâm:
- Lý Thuyết Phương Trình Đường Tròn Lớp 10 Môn Toán
- Tổng quan lý thuyết về hàm số lớp 10, các dạng bài tập hàm số
- Tổng hợp các dạng toán hình học không gian thường gặp nhất
- Ma trận đề thi trung học phổ thông quốc gia 2023 cập nhật các môn
Các Bài Viết Liên Quan





