Tổng quan lý thuyết về hàm số lớp 10, các dạng bài tập hàm số

Lý thuyết hàm số 10 là một phần quan trọng trong toán học. Các hàm số phức tạp có thể được phân tích và hiểu bằng cách sử dụng các khái niệm và phương pháp đặc biệt. Bài viết này sẽ khám phá những khía cạnh cơ bản của lý thuyết hàm số 10 và cung cấp ví dụ về các dạng bài tập liên quan đến chủ đề này.

1. Lý thuyết hàm số lớp 10

1.1. Hàm số là gì?

Giả sử D ⊂ R, D ≠ ϕ. Hàm số xác định trên D theo quy tắc f, x ∈ D và y ∈ R. Ta có ký hiệu:

• f: D → R
  x ↦ y = f ( x )

D: Tập hợp xác định; x: Biến số; y0= f(x0) tại x = x0.

Hàm có thể ở dưới dạng công thức, biểu đồ hoặc bảng.

Lưu ý: Nếu hàm số dưới dạng công thức nhưng không cho tập xác định thì ngầm hiểu rằng tập xác định D là các số x ∈ R, đáp ứng điều kiện các phép toán trong công thức có nghĩa. 

1.2 Đồ thị của hàm số 10

Đồ thị hàm số:

f: D → R

x ↦ y = f ( x )

là tập hợp các điểm (x, f ( x )), x ∈ D trên mặt phẳng tọa độ.

Có 2 dạng đồ thị hàm số 10 mà học sinh cần lưu ý:

Đồ thị hàm số bậc nhất: y = ax + b có dạng đường thẳng.

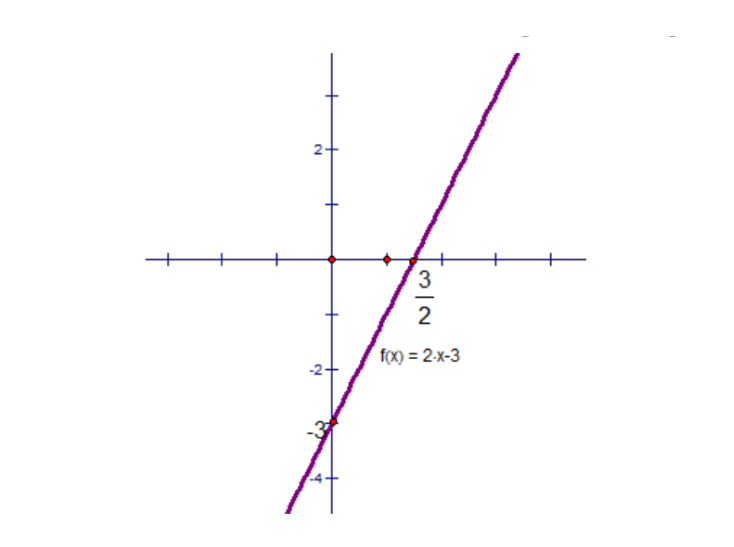
Đồ thị hàm số bậc nhất

Đồ thị hàm số bậc hai: y = ax2 có dạng đường parabol. 

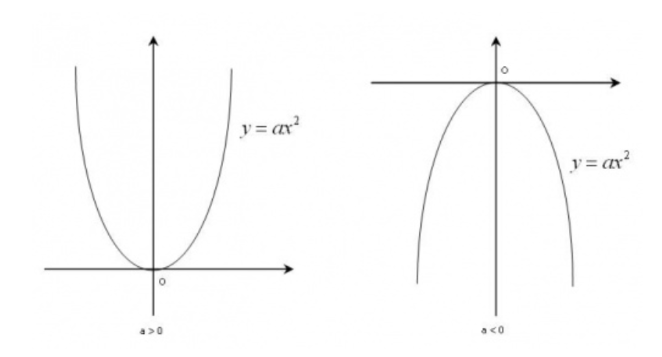
Đồ thị hàm số bậc hai

>> Có thể bạn quan tâm:

• Cách vẽ đồ thị hàm số toán 10 – bài tập kèm giải chi tiết 2023
• Lý thuyết hệ trục tọa độ lớp 10 chi tiết 2023
• Lý thuyết Hàm số và đồ thị lớp 10 – SGK Toán 10 Cánh Diều 2023

1.3 Bảng biến thiên của hàm số

• Hàm số y = f ( x ) là đồng biến (tăng) trên khoảng (a; b) nếu với mọi x1, x2 ∈ (a; b) mà: x1 < x2 ⇔ f ( x1 ) < f ( x2 ). 
• Hàm số y = f ( x ) là nghịch biến (giảm) trên khoảng (a; b) nếu với mọi x1, x2 ∈ (a; b) mà: x1 < x2 ⇔ f ( x1 ) > ( x2 ). 

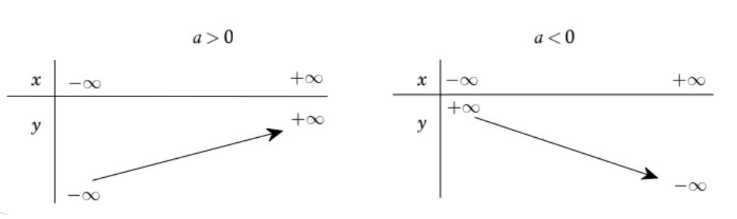
Bảng biến thiên hàm số 10

 

 

1.4 Xét tính chẵn lẻ của hàm số 10

Cho hàm số y = f ( x ), thuộc tập hợp D, ta có:

• Hàm số y = f ( x ) là hàm chẵn nếu x ∈ D, −x ∈ D và f ( −x ) = f ( x ).
• Hàm số y = f ( x ) là hàm lẻ nếu x ∈ D, −x ∈ D và f ( −x ) = − f ( x ).

Đồ thị hàm số 10 tính chẵn lẻ có dạng như sau:

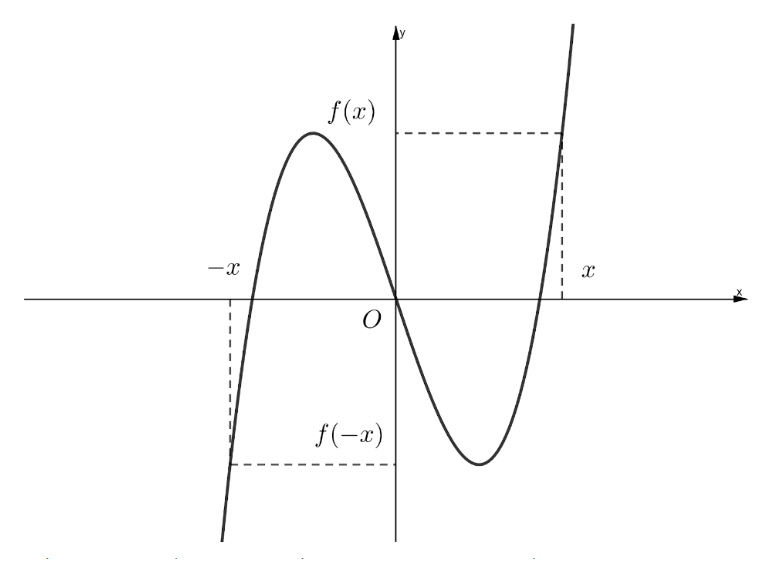
Đồ thị chẵn có trục tung là trục đối xứng

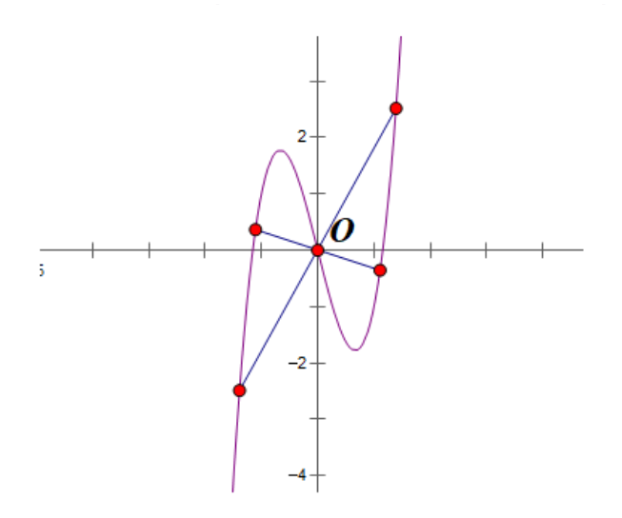
Đồ thị lẻ có gốc tọa độ là tâm đối xứng

2. Các dạng bài tập hàm số lớp 10

2.1 Dạng 1: Tính giá trị của hàm số tại một điểm

Phương pháp giải: Tính giá trị hàm số y = f ( x ) tại x = a. Ta thực hiện thay x = a vào biểu thức hàm y để được f ( a ). Tính giá trị f ( a ) sẽ ra giá trị hàm số y = f ( x ) tại x = a.

Ví dụ 1: Cho hàm số dưới đây. Yêu cầu tính giá trị f ( 1) và f ( -2 )

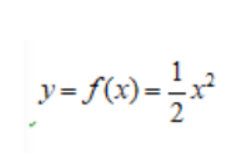
Hướng dẫn giải:

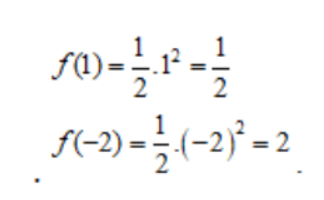
Ví dụ 2: Cho hàm số dưới đây. Yêu cầu tính f (x) tại x=2 và x=4. 

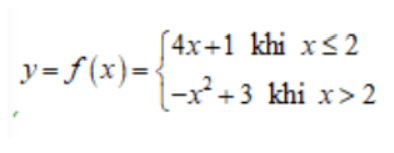
Hướng dẫn giải:

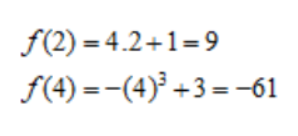
Ví dụ 3: Một vật rơi tự do ở khoảng cách 400m so với mặt đất. Quãng đường chuyển động S(m) của vật phụ thuộc vào thời gian t (giây). Công thức s = 4t2. Tính thời gian vật tiếp đất. 

Khoảng cách giữa vật và đất là 400m. Thay s=400, ta được:

400 = 4t2 ⇔ t2 = 100, vậy t = 10 (giây). 

2.2 Dạng 2: Tìm tập xác định của hàm số

Phương pháp giải: Đối với dạng bài tìm tập xác định hàm số 10, học sinh cần vận dụng lý thuyết. Theo đó, tập xác định của hàm y = f ( x ) là tập hợp các giá trị x sao cho f ( x ) có nghĩa. 

Một số tập xác định đặc biệt mà học sinh cần ghi nhớ:

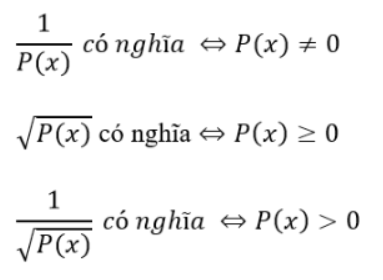
Ví dụ 1: Tìm tập xác định của hàm số:

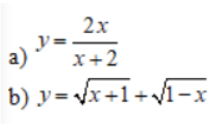
Hướng dẫn giải:

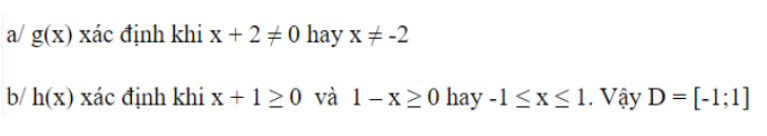
2.3 Dạng 3: Xác định tính chẵn lẻ của hàm số

Phương pháp giải: 

Bước 1: Xét tập D là tập đối xứng.

Bước 2: Tính f ( −x ):

• Nếu f ( −x ) = f ( x ) thì hàm chẵn.
• Nếu f ( −x ) = −f ( x ) thì hàm lẻ. 

Bước 3: Vẽ đồ thị hàm số.

Ví dụ 1: Tính chẵn lẻ của hàm số sau:

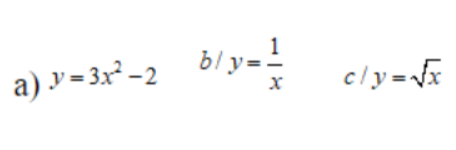
Hướng dẫn giải:

Trên đây Marathon Education đã tổng hợp lý thuyết và các dạng bài tập hàm số 10. Đối với dạng bài hàm số 10, học sinh cần nắm vững lý thuyết và cách vận dụng linh hoạt để giải quyết các bài tập thực tế. Marathon chúc các em thành công!

>> Có thể bạn quan tâm:

• Lý thuyết Hoán vị chỉnh hợp tổ hợp lớp 10 bài 24
• Tổng hợp các dạng hình không gian thường gặp nhất
• Ma trận đề thi THPT quốc gia 2023 cập nhật các môn
• Lý thuyết và cách giải bài tập hàm số bậc hai lớp 10