Lý thuyết Hệ trục tọa độ lớp 10 (hay, chi tiết) 2023
Hệ trục tọa độ lớp 10 là một khái niệm cơ bản và quan trọng trong chương trình toán cấp 3. Đây là một hệ thống giúp chúng ta xác định vị trí và mối quan hệ không gian giữa các điểm trong mặt phẳng. Trong bài viết này, chúng ta sẽ tìm hiểu về cách xây dựng và sử dụng trục tọa độ, cùng với những ứng dụng thực tế quan trọng của nó.
1. Trục và độ dài đại số trên trục
a. Trục tọa độ là đường thẳng trên đó đã có 1 điểm O gọi là gốc và 1 vectơ đơn vị ký hiệu là 
Ta gọi trục đó là (O; ).
b. Cho M là điểm tùy ý nằm trên (O; ). Lúc này, có duy nhất một số k sao cho 
Ta gọi số k là tọa độ điểm M đối với trục đã cho.
c. Cho 2 điểm A và B nằm trên trục (O; ). Lúc này, có duy nhất một số a sao cho 
Ta gọi a là độ dài số của vector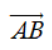 
, kí hiệu: a = .
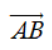- Nếu 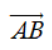cùng hướng vớ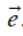i thì 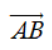= AB. Nếu 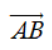ngược hướng vớ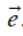i thì 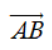= –AB.
- Nếu 2 điểm A, B nằm trên (O; 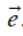) có tọa độ lần lượt là a, b thì 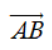= b – a
2. Hệ trục tọa độ
a. Khái niệm:
Hệ trục tọa độ lớp 10 (O;
; 
) gồm 2 trục là (O; ) và ( O; ) vuông góc với nhau. Điểm O chung là gốc tọa độ. (O; ) là trục hoành, ký hiệu: Ox; ( O; ) là trục tung, ký hiệu: Oy. Vectơ ; là vectơ đơn vị trên trục hoành và trục tung,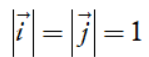
. Hệ trục tọa độ (O; ; ) được ký hiệu là Oxy.
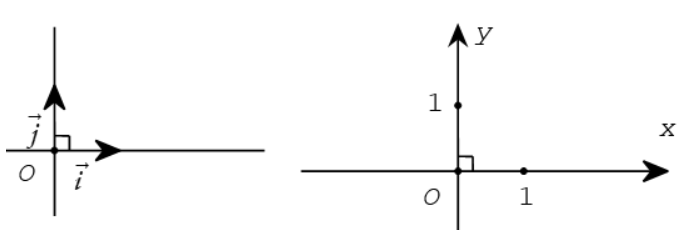
Hệ trục tọa độ Oxy
Mặt phẳng chứa hệ trục tọa độ lớp 10 Oxy được gọi là mặt phẳng Oxy.
b. Tọa độ của vectơ
Trong mặt phẳng Oxy, cho vectơ 
và gọi A1, A2 lần lượt là hình chiếu vuông góc của A lên Ox và Oy. Ta có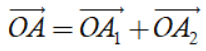 
và cặp số duy nhất (x; y) để 
.
Như vậy: 
Cặp số (x; y) được gọi là tọa độ của vectơ 
, viết là: = (x; y) hoặc (x; y). Số x gọi là hoành độ, số y gọi là tung độ của vectơ .
Như vậy: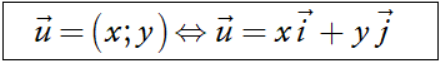 
Nhận xét: 2 vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
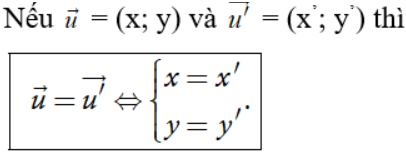
c. Tọa độ của một điểm
Trong mặt phẳng Oxy cho điểm M tùy ý. Tọa độ vectơ 
được gọi là tọa độ của điểm M đối với hệ trục Oxy.
Như vậy, (x; y) là tọa độ điểm M khi và chỉ khi , ta viết M(x; y) hoặc M = (x; y). Số x là hoành độ, y là tung độ của M.
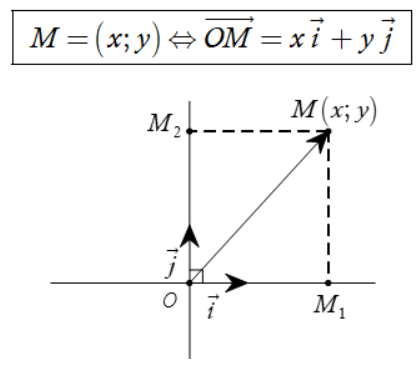
Nếu MM1 ⊥ Ox, MM2 ⊥ Oy thì 
- Liên hệ giữa tọa độ điểm và tọa độ vectơ
Cho hai điểm A(xA, yA) và B(xB, yB). Ta có:
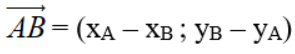
3. Tọa độ của tổng, hiệu ,tích của một số với một vectơ
Tọa độ các vectơ 
Ta có:
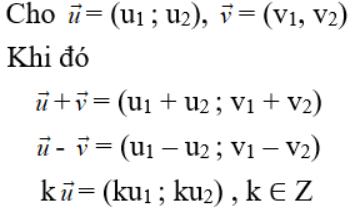
Nhận xét: 2 vectơ 
cùng phương khi và chỉ khi có 1 số k sao cho u1 = kv1 và u2 = kv2.
4. Tọa độ của trung điểm của đoạn thẳng và tọa độ trọng tâm của tam giác
a. Cho đoạn thẳng AB có A(xA, yA) và B(xB, yB). Ta dễ dàng tìm được trung độ điểm I(xI, yI) của đoạn AB là:
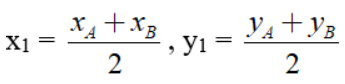
b. Cho tam giác ABC có A(xA, yA), B(xB, yB), C(xC, yC). Khi đó tọa độ trọng tâm G(xG, yG) của tam giác ABC được tính như sau:
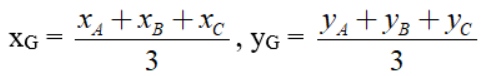
Qua bài viết này, Marathon Education đã cùng nhau khám phá tổng quan về hệ trục tọa độ lớp 10. Trục tọa độ không chỉ giúp chúng ta biểu diễn và hiểu sâu hơn về không gian, mà còn là cơ sở để nắm vững nhiều kiến thức toán học quan trọng trong tương lai.
>> Có thể bạn quan tâm:
- Lý thuyết Hàm số và đồ thị lớp 10 – SGK Toán 10 Cánh Diều 2023
- Cách vẽ đồ thị hàm số lớp 10 – bài tập kèm giải chi tiết 2023
- Tổng quan lý thuyết về toán 10 hàm số, các dạng bài tập hàm số
- Ma trận đề thi THPT quốc gia các môn cập nhật 2023
Các Bài Viết Liên Quan
