Cách vẽ đồ thị hàm số lớp 10 – bài tập kèm giải chi tiết
1. Tổng hợp lý thuyết hàm số lớp 10
1.1. Định nghĩa
Đồ thị hàm số được định nghĩa như sau:
Cho D là tập hợp con khác tập rỗng thuộc $\mattbb{R}$. Hàm số f xác định trên tập D là một quy tắc cho tương ứng với mỗi số $x\in D$ với một và chỉ một số thực y gọi là giá trị của hàm số f tại x, ký hiệu là $y=f(x)$.
Tập D được gọi là tập xác định của hàm số y (tập này có ý nghĩa đặc biệt quan trọng trong việc làm nền tảng vẽ đồ thị hàm số lớp 10), x là biến số.
Tóm lại, ta có công thức như sau:
F: D → R
x → y = f (x)
1.2 Xét biến thiên hàm số 10
Xét hàm số f (x) trên tập D, ta sẽ có:
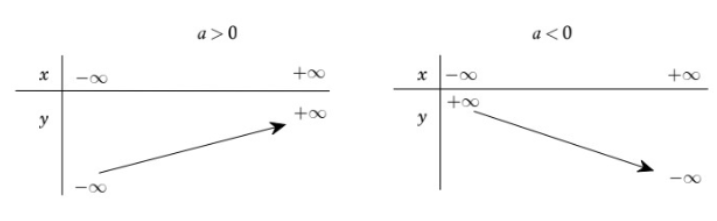
- Hàm số y = f (x) đồng biến (tăng) trên khoảng (a;b) khi: x1, x2 ∈ (a;b): x1<x2 ⇒ f (x1) < f (x2)
- Hàm số y = f (x) nghịch biến (giảm) trên khoảng (a;b) khi: x1, x2 ∈ (a;b): x1<x2 ⇒ f (x1) > f(x2)
Hình ảnh bảng biến thiên tổng quát cần xét trước khi thực hiện vẽ đồ thị hàm số lớp 10:
2. Chi tiết cách vẽ hàm số lớp 10
2.1 Cách vẽ hàm số bậc nhất
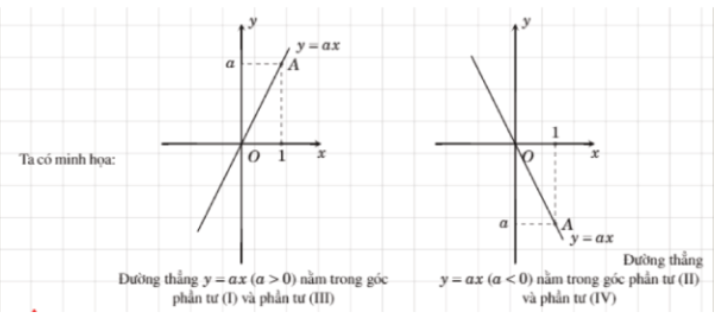
Trường hợp 1: y = ax, (a ≠0)
Đồ thị hàm số y = ax, (a ≠0) là đường thẳng đi qua đi qua gốc tọa độ và điểm A (1;0). Để vẽ đồ thị hàm số này, thực hiện như sau:
- Bước 1: Xác định vị trí điểm A (1;a)
- Bước 2: Nối O với A, ta được đồ thị hàm số y = ax
Lưu ý:
- Đồ thị hàm số y = x là đường phân giác của góc phần tư thứ I, III
- Đồ thị hàm số y = -x là đường phân giác của góc phần tư thứ II, IV
Trường hợp 2: y = ax+b, (a ≠0)
Đồ thị hàm số y = ax+b, (a ≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b. Vẽ đường thẳng này như sau:
- Bước 1: Xác định điểm M (0;b)
- Bước 2: Đường thẳng đi qua điểm M song song với đường y=ax thì y = ax+b, (b ≠0)
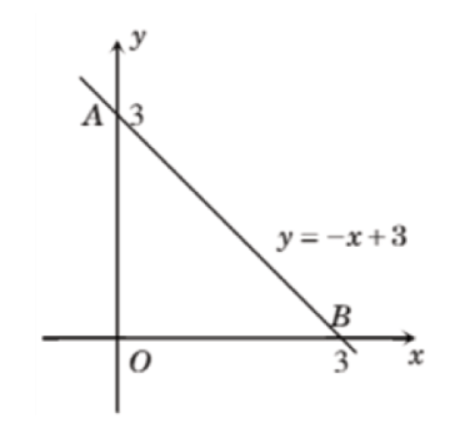
Ví dụ 1: Cho hàm số y = -x + 3
- Xác định giao điểm của đồ thị hàm số với trục tung và trục hoành, vẽ đồ thị hàm số này
- Gọi A và B lần lượt theo thứ tự của hai giao điểm kể trên, tính diện tích tam giá OAB (trong đó O là gốc tọa độ)
- Gọi α là góc nhọn được tạo nên bởi đồ thị hàm số với trục Ox. Tính tanα, từ đó suy ra số đo góc α
- Dựa trên đồ thị, tiếp tục tìm x để y > 0, y0
Cách giải:
a.
- Đồ thị cắt trục Oy tại A, ta có:
x= 0 ⇒ y = -0 + 3 = 3 ⇒ A (0;3)
- Đồ thị cắt trục Ox tại B, ta có
y=0 ⇒ 0= -x +3 ⇒ x = 3 ⇒ B (3;0)
b. Ta có:
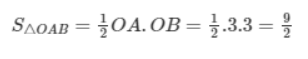
c. Xét:
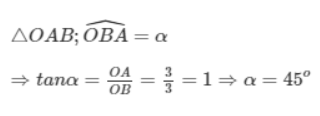
d. Từ đồ thị suy ra

Ví dụ 2: Cho hàm số y = ax – 3a
a. Xác định giá trị của a để đồ thị hàm số đi qua điểm A (0;4). Vẽ đồ thị hàm số a vừa tìm được
b. Tính khoảng cách từ gốc tọa độ đến đường thẳng tìm được ở câu hỏi a
Cách giải
a. Đồ thị hàm số đi qua điểm A (0;4) khi và chỉ khi 4 = a.0 – 3a = – 4a = – 4/3
Vậy hàm số dạng có dạng y = – 4/3x + 4
Ta cần lấy thêm điểm B (3;0) để vẽ đồ thị hàm số:
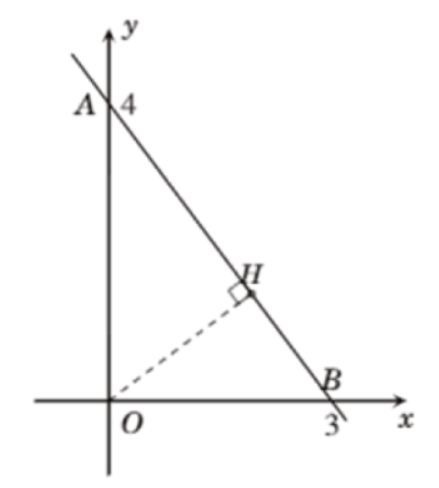
b. Gọi H là hình chiếu vuông góc của O trên đường thẳng AB. Trong tam giác OAB, ta có:
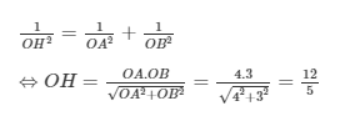
2.2 Cách vẽ hàm số bậc hai
Để vẽ đồ thị hàm số bậc hai, ta có thể dùng 1 trong 2 cách sau tùy từng trường hợp:
Cách 1: Có thể áp dụng cho mọi trường hợp
- Bước 1: Xác định tọa độ đỉnh 1
- Bước 2: Vẽ trục đối xứng của đồ thị
- Bước 3: Xác định tọa độ các giao điểm của Parabol lần lượt với trục tung và trục hoành (nếu có)
Cách 2: Dùng khi đồ thị hàm số có dạng y = ax2
Đồ thị hàm số 2y= ax2 + bx + c (a ≠0) được suy ra từ đồ thị hàm số y = ax2 theo cách:
- Nếu b2a > 0 thì tịnh tiến song song với trục hoành b2a đơn vị về phía bên trái, về bên phải nếu b2a<0
- Nếu -4a>0 thì tịnh tiến song song với trục tung – 4a đơn vị lên trên, xuống dưới nếu -4a <0
Đồ thị hàm số y = ax2 + bx + c (a ≠0) có dạng như sau:
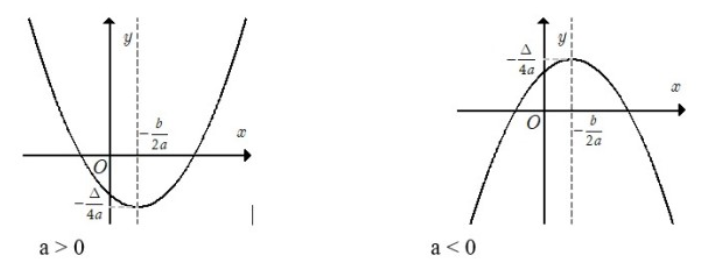
Đồ thị hàm số bậc 2 lớp 10 y = ax2 + bx + c (a ≠0) là đường parabol với đặc điểm:
- Đỉnh: I (-b/2a;-/4a)
- Trục đối xứng: Đường thẳng x= -b/2a
- Nếu a<0, phần lõm của parabol quay xuống phía dưới, nếu a>0, phần lõm của parabol hướng lên trên
- Giao điểm với trục tung: A(0;c)
- Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình ax2 + bx + x = 0
Ví dụ: Vẽ đồ thị của hàm số y = ax2 + 3x + 2
Cách giải:
Ta có:
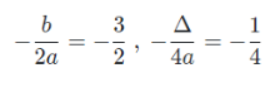
Bảng biến thiên của tần số
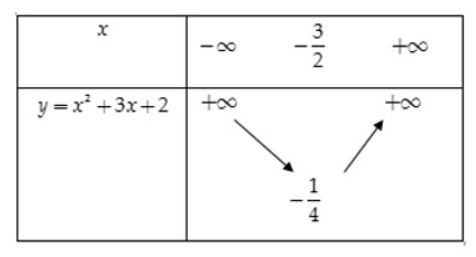
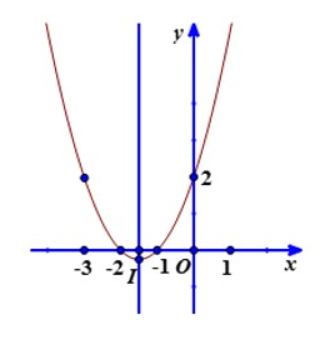
Suy ra: Đồ thị hàm số y = ax2 + 3x + 2 có đỉnh I(-3/2;-¼) và lần lượt đi qua các điểm A (-2;0), B (-1;0), C (0,2), D(-3,2)
Đồ thị hàm số y = ax2 + 3x + 2 nhận đường x=-3/2 làm trục đối xứng và có phần lõm hướng lên trên
2.3 Cách vẽ đồ thị hàm số tuyệt đối
Có 2 trường hợp để vẽ đồ thị hàm số lớp 10 dạng trị tuyệt đối.
Trường hợp 1: Đồ thị hàm số bậc nhất chứa dấu trị tuyệt đối f(x)
Cách 1: Sử dụng quy tắc phá dấu trị tuyệt đối, sau đó tiến hành vẽ
Cách 2:
- Bước 1: Vẽ đồ thị hàm số y = f (x)
- Bước 2: Giữ nguyên phần đồ thị phía trên trục Ox của y = f (x) (P1)
- Bước 3: Lấy đối xứng phần đồ thị phía dưới trục Ox của y = f (x) lên phía trên Ox ta được (P2)
- Bước 4: Đồ thị f (x) là P1 và P2
Trường hợp 2: Đồ thị hàm số bậc nhất chứa dấu giá trị tuyệt đối f (x)
Cách giải:
- Bước 1: Vẽ đồ thị hàm số y = f (x)
- Bước 2: Lấy đối xứng qua Oy phần đồ thị bên phải Oy của y = f(x)
- Bước 3: Đồ thị y = f (x) là phần bên phải và phần lấy đối xứng
Trường hợp 3: Đồ thị hàm số bậc hai chứa trị tuyệt đối
Để vẽ đồ thị hàm số bậc hai chứa trị tuyệt đối y = ax2 + bx + c, làm theo các bước:
Bước 1:
Vẽ đồ thị (P) = y = ax2 + bx + c
Ta có:
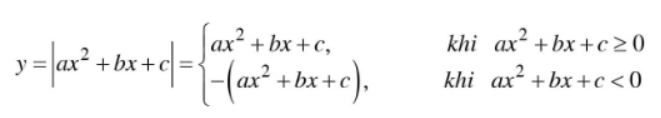
Vậy đồ thị hàm số gồm 2 phần:
- Phần 1: Đồ thị hàm số bậc 2 (P) lấy phần phía trên trục Ox
- Phần 2: Lấy đối xứng phần đồ thị (P) phía dưới trục Ox qua trục Ox
Ví dụ: Vẽ những đồ thị hàm số sau đây:
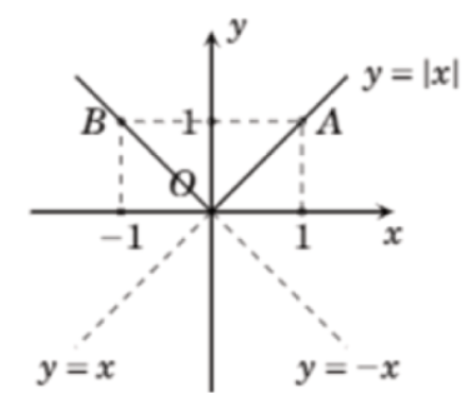
- y = |x|
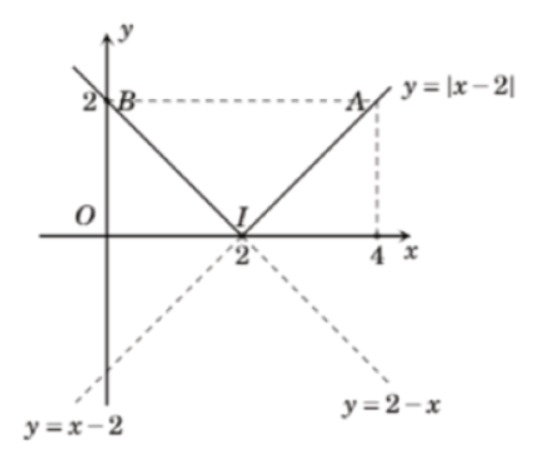
- y = |x-2|
- y = |x-1| + 2
Cách giải:
a. Ta có:
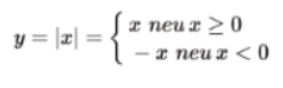
Đồ thị hàm số là tia OA với A(1,1) và OB với B (-1,1)
b. Ta có
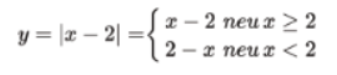
Đồ thị hàm số là 2 tia IA với I (2;0) và IB với B(0;2)
c. Ta có
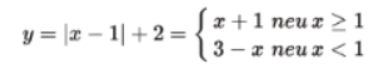
Đồ thị hàm số là 2 tia IA với A (1;2) và IB với B (0;3)
3. Bài tập áp dụng cách vẽ đồ thị hàm số lớp 10
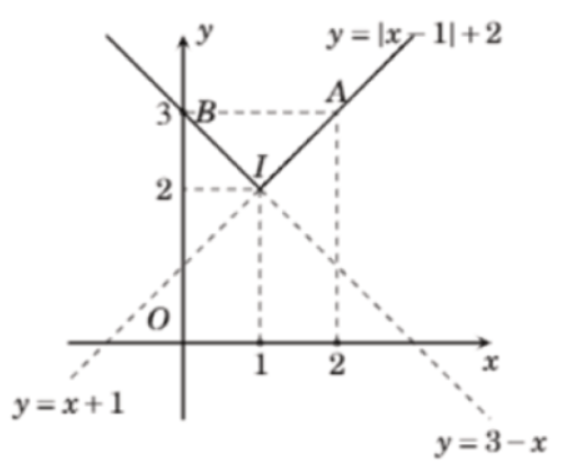
Bài 1: Vẽ đồ thị các hàm số sau đây:
Cách giải:
- Với x0 đồ thị hàm số y = 2x là đường thẳng đi qua 2 điểm A (1;2) và điểm O (0;0) nằm bên phải trục tung
Với x < 0 đồ thị hàm số y = – x là đường thẳng đi qua B (-1;1) và C (-2;2) nằm phía bên trái trục tung
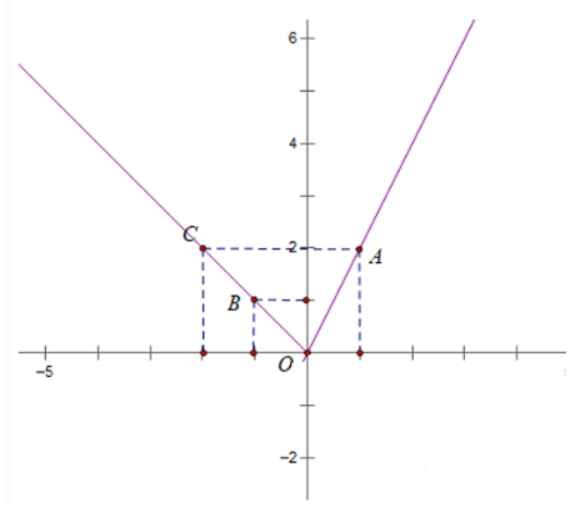
2. Vẽ 2 đường thẳng y = -3x + 3 và đường y = 3x – 3, lấy phần đường thẳng nằm trên trục hoành
Bài 2: Lập bảng biến thiên và vẽ đồ thị các hàm số sau đây:
- y = 3x + 6
- y = -1x/2 + 3/2
Cách giải:
- Tập xác định R, a = 3>0 ⇒ Hàm số đồng biến trên R. Lập bảng biến thiên
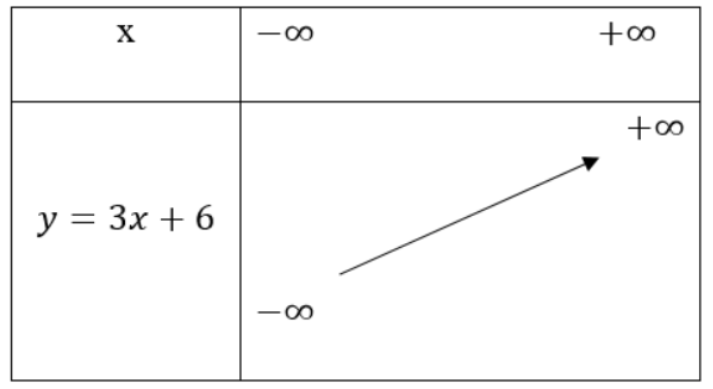
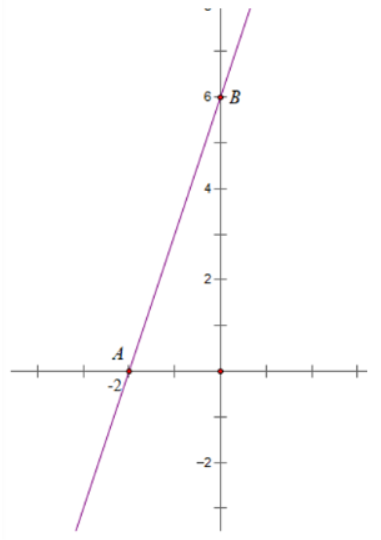
Đồ thị hàm số y = 3x + 6 đi qua 2 điểm A (-2;0), B (0;6)
2. Tập xác định D = R, a = (-1)/2<0 ⇒ Hàm số nghịch biến trên R. Lập bảng biến thiên
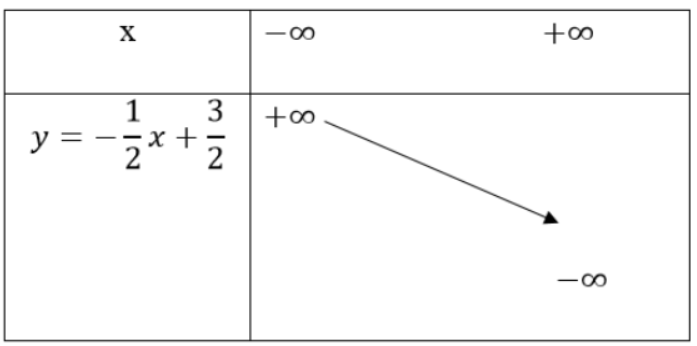
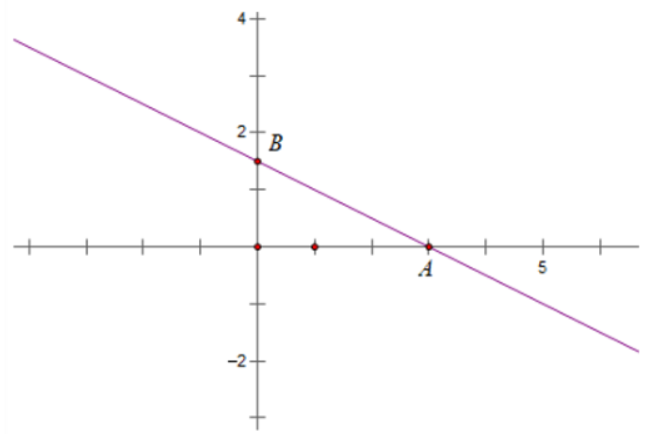
Đồ thị hàm số y = -1x/2 + 3/2 đi qua 2 điểm A (3;0), B (0; 3/2)
Bài 3: Cho đồ thị hàm số có đồ thị (C) hình vẽ bên dưới
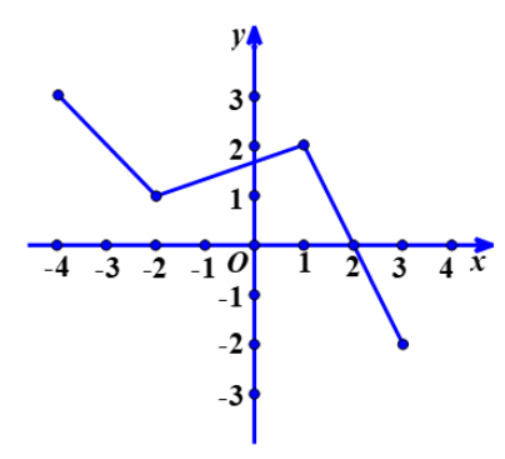
a. Lập bảng biến thiên của hàm số trên [-3;3]
b. Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên [-4;2]
Cách giải:
- Lập bảng biến thiên của hàm số trên đoạn [-3;3]:
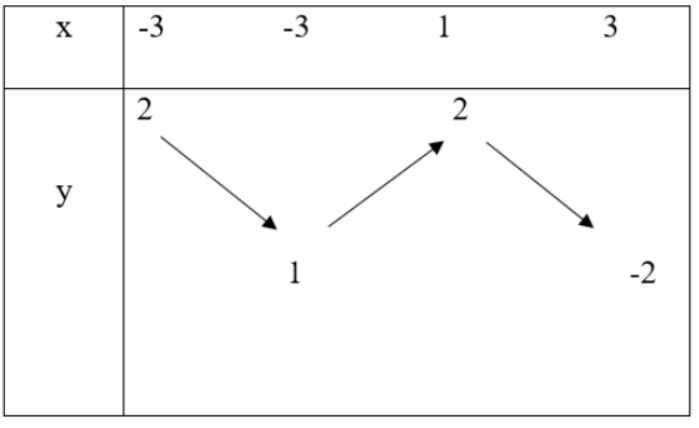
2. Căn cứ theo đồ thị hàm số đề bài, ta có:

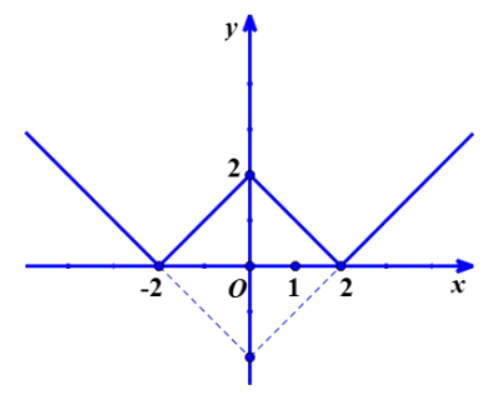
Bài 4: Vẽ đồ thị của những hàm số trị tuyệt đối sau đây
a. y = |x| – 2
b. y = ||x| – 2|
Cách giải:
Có 2 cách giải như sau:
Cách 1: Ta có:
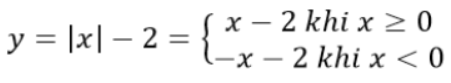
Vẽ đường thẳng y = x – 2 đi qua 2 điểm A (0;-2), B (2;0) và lấy phần đường thẳng bên phải của trục tung
Vẽ đường thẳng y = – x – 2 đi qua 2 điểm A (0;-2), B (-2;0) và lấy phần đường thẳng bên phải của trục tung
Cách 2: Đường thẳng d: y = x – 2 đi qua A (0;-2), B (2;0)
Vậy đồ thị hàm số y = |x| – 2 chính là phần đường thẳng d nằm bên phải của trục tung và phần đối xứng của nó qua trục tung
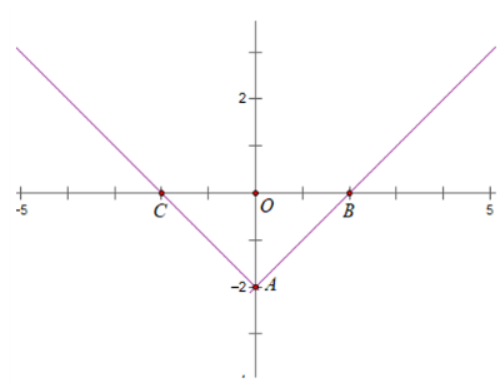
- Đồ thị y = ||x| – 2| gồm phần:
Giữ nguyên đồ thị hàm số y = |x| – 2 ở phía trên trục hoành
Lấy đồi xứng phần đồ thị hàm số y = ||x| – 2| ở phía dưới trục hoành
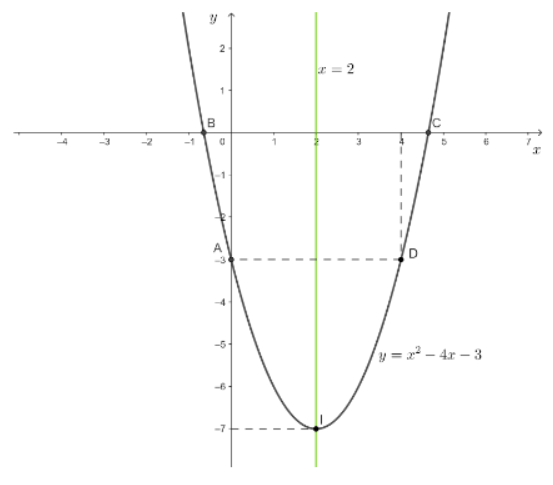
Bài 5: Vẽ đồ thị những hàm số bậc hai sau:
a. y = x2 – 4x – 3
b. y = x2 + 2x + 1
Cách giải:
- Với hàm số y = x2 – 4x – 3 ta có:
a = 1, b = – 4, c = – 3, = (-4)^2 – 4.1.(-3) = 28
- Tọa độ đỉnh: I (2;-7)
- Trục đối xứng: x = 2
- Giao điểm của parabol với trục tung: A (0;-3)
- Giao điểm của parabol với trục hoành: B (2; -7;0) và C (2+7;0)
- Điểm đối xứng với A (0;-3) qua trục x = 2 là D (4;-3)
- Vì A>0 nên phần lõm đồ thị sẽ hướng lên trên
- Đồ thị của hàm số y = x2 – 4x – 3 có dạng
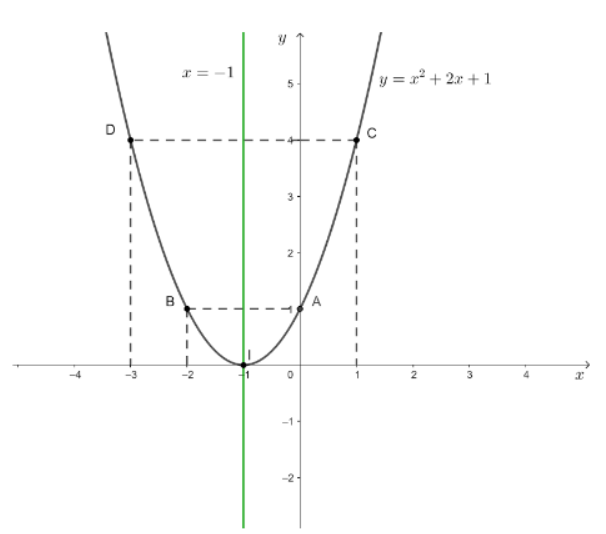
2. Với hàm số y = x2 + 2x + 1 ta có:
a=1, b=2, c=1 = 2^2 – 4.1 + 1 = 0
- Tọa độ đỉnh: I (-1,0)
- Trục đối xứng: x = – 1
- Giao điểm của parabol với trục tung là (0;1)
- Giao điểm của parabol với trục tung là đỉnh I
- Điểm đối xứng với A (0;1) qua trục đối xứng x = -1 là B (-2;0)
- Lấy điểm C (1;4) thuộc đồ thị hàm số đề bài, điểm đối xứng C qua trục x = – 1 là điểm D (-3;4)
- Do a > 0 nên phần lõm của đồ thị hàm số sẽ hướng lên trên
- Đồ thị hàm số có dạng như sau:
Marathon Education đã cung cấp đầy đủ lý thuyết và hướng dẫn giải bài tập vẽ đồ thị hàm số lớp 10 giúp các em học sinh nắm vững hơn về học phần này trong chương trình học lớp 10.
>> Có thể bạn quan tâm:
- Lý thuyết hệ trục tọa độ lớp 10 môn Toán 2023
- Lý thuyết Toán 10 bài hàm số bậc hai và cách giải bài tập
- Tổng quan lý thuyết về hàm số lớp 10, các dạng bài tập hàm số 2023
- Ma trận đề thi Trung học phổ thông quốc gia 2023 cập nhật các môn
Các Bài Viết Liên Quan





