Lý Thuyết Về Phép Biến Hình Lớp 11
Trong bài viết dưới đây, Marathon Education sẽ chia sẻ đến các em các nội dung liên quan đến phép biến hình lớp 11 bao gồm các định nghĩa, các phép biến hình thường gặp, dạng toán quỹ tích bằng phép biến hình với bài tập ví dụ và lời giải chi tiết. Các em hãy dành thời gian học và làm bài tập thường xuyên để nắm vững những kiến thức này.
>>> Xem thêm: Chia Sẻ Bí Quyết Học Tốt Hình Học Không Gian Lớp 11
>>> Xem thêm: Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10
>>> Xem thêm: Học Online Toán 11 Bứt Phá Điểm Số Với Marathon Education
Định nghĩa phép biến hình lớp 11
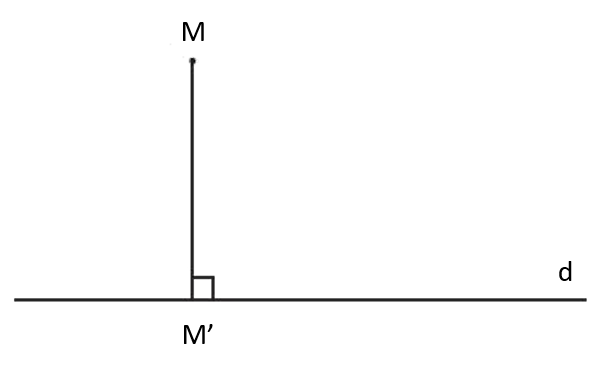
Phép biến hình được định nghĩa dựa trên quy tắc tương ứng mỗi điểm M trong mặt phẳng ta xác định duy nhất được một điểm M’ trong cùng mặt phẳng đó. Đậy được gọi là phép biến hình trong mặt phẳng.
- Nếu ký hiệu phép biến hình là F thì ta viết F(M) = M’ hay M’ = F(M) và gọi điểm M’ là ảnh của điểm M qua phép biến hình F.
- Nếu A là một hình trong mặt phẳng thì ta kí hiệu A’ = F(A) là tập các điểm M’ = F(M), với mọi điểm M thuộc A. Khi đó ta nói F biến hình A thành hình A’, hay hình A’ là ảnh của hình A qua phép biến hình F.
- Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.
Phép dời hình
Định nghĩa:
- Phép dời hình là phép biến hình bảo toàn khoảng cách giữa 2 điểm bất kì.
- Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép dời hình.
- Phép biến hình chính là kết quả của việc thực hiện liên tiếp hai phép dời hình liên tiếp.
- Hình minh họa phép dời hình:
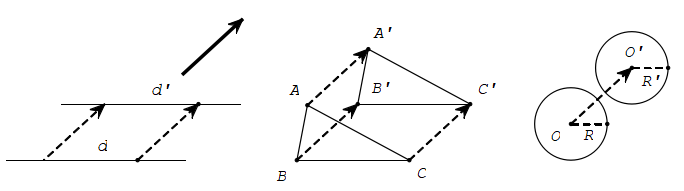
Tính chất: Phép dời hình
- Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
- Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng có độ dài không đổi.
- Biến tam giác thành tam giác có độ dài các cạnh không đổi, biến góc thành góc có số độ không đổi.
- Biến đường tròn thành đường tròn có cùng bán kính.
Phép tịnh tiến
Định nghĩa:
\begin{aligned}
&\footnotesize\bull\text{Trong mặt phẳng cho vectơ }\vec{v}.\text{ Phép biến hình biến mỗi điểm M thành điểm M’ sao cho vectơ }\overrightarrow{MM’} = \vec{v} \\
&\footnotesize\text { được gọi là phép tịnh tiến theo vectơ }\vec{v}.\\
&\footnotesize\bull\text {Phép tịnh tiến theo vectơ } \vec{v} \text{ thường được kí hiệu là }T_{\vec{v}},\ \vec{v} \text{ được gọi là vectơ tịnh tiến.}\\
&\footnotesize\bull\text {Hình minh họa phép tịnh tiến:}
\end{aligned}
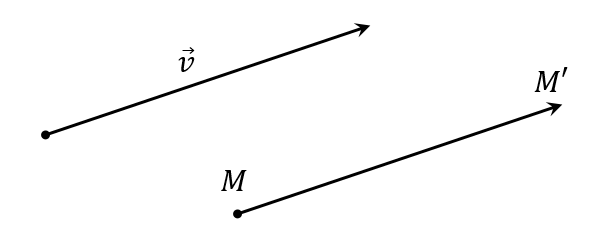
Biểu thức toạ độ:
\begin{aligned}
&\footnotesize\text{Trong mặt phẳng tọa độ Oxy cho vectơ }\vec{v}=(a;b)\text{ và điểm M(x;y). Nếu M’(x’,y’) là ảnh của M qua phép tịnh }\\
&\footnotesize\text{tiến theo }\vec{v}. \text{ Khi đó vectơ } \overrightarrow{MM’}\text{ hay }T_{\vec{v}}(M)=M' \text{ có biểu thức tọa độ là:}\begin{cases}x'=x+a\\y'=y+b \end{cases}
\end{aligned}
Tính chất:
\begin{aligned}
&\footnotesize\bull\text{Nếu }T_{\vec{v}}(M)=M',\ T_{\vec{v}}(N)=N' \text{ thì }\overrightarrow{MN}=\overrightarrow{M'N'} \Rightarrow M'N'=MN\\
&\footnotesize\bull\text{Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng ban đầu, biến}\\
&\footnotesize\text{đoạn thẳng thành đoạn thẳng có độ dài không đổi, biến tam giác thành tam giác bằng nó, biến đường tròn }\\
&\footnotesize\text{thành đường tròn cùng bán kính.}
\end{aligned}
Phép đối xứng trục
Định nghĩa:
- Phép đối xứng trục là phép biến hình mỗi điểm M thành M’ sao cho d là đường trung trực của MM’ hay điểm M’ đối xứng với điểm M qua trục d.
- Ký hiệu: Đd (M) = M’
- Hình minh hoạ phép đối xứng trục:
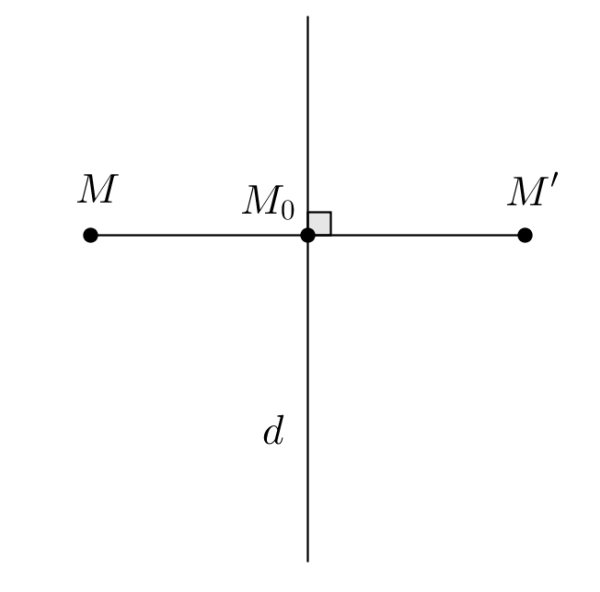
Biểu thức toạ độ:
Nếu d ≡ Ox (đường thẳng d trùng với trục hoành). Gọi M’(x’; y’) = ĐOx[M(x,y)] thì:
\begin{cases}
x'=x\\y'=-y
\end{cases}
Nếu d ≡ Oy (đường thẳng d trùng với trục tung). Gọi M’(x’; y’) = ĐOy[M(x,y)] thì:
\begin{cases}
x'=-x\\y'=y
\end{cases}
Tính chất:
- Với 2 điểm ban đầu cho trước, khoảng cách giữa 2 điểm trong phép đối xứng trục luôn không đổi.
- Phép đối xứng trục biến đường thẳng thành đường thẳng song song, đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
Phép đối xứng tâm
Định nghĩa:
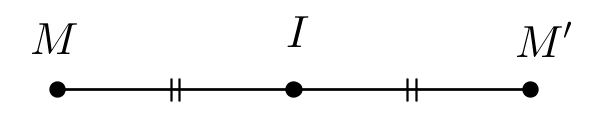
- Cho điểm I trong mặt phẳng bất kỳ. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành M’ sao cho I là trung điểm của MM’ được gọi là phép đối xứng tâm I.
- Điểm I được gọi là tâm đối xứng.
- Phép đối xứng tâm I thường được kí hiệu là ĐI.
- Hình minh hoạ phép đối xứng tâm:
Biểu thức toạ độ:
Với O(0;0), ta có M(x’; y’) = ĐO[M(x;y)] thì:
\begin{cases}
x'=-x\\y'=-y
\end{cases}
Với I(a; b), ta có M(x’; y’) = ĐI(x’; y’) thì:
\begin{cases}
x'=2a-x\\y'=2b-y
\end{cases}
Tính chất:
\footnotesize\bull\ \text{Nếu } Đ_I(M) = M’ \text{ và } Đ_I(N) = N' \text{ thì }\overrightarrow{MN}=\overrightarrow{M'N'} \Rightarrow M'N'=MN.
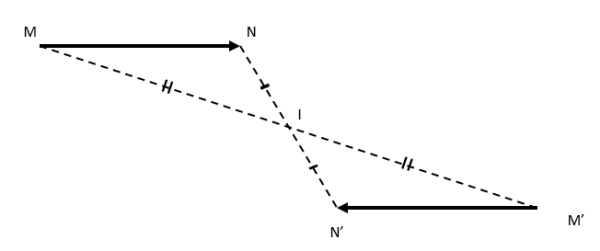
- Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.

Phép quay
Định nghĩa:
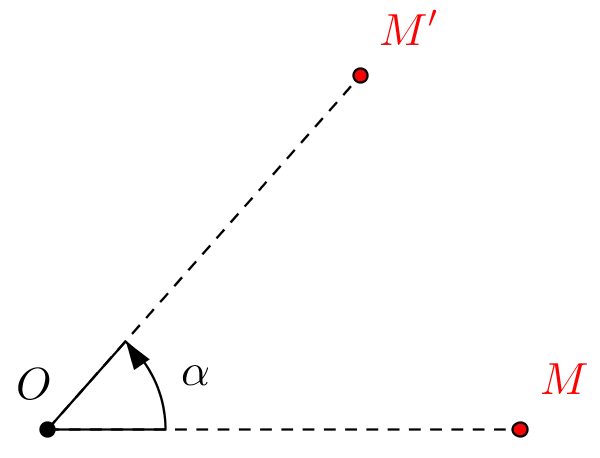
- Trong mặt phẳng, cho điểm O và góc α. Phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc (OM; OM’) bằng α được gọi là phép quay tâm O góc α.
- Điểm O được gọi là tâm quay, α được gọi là góc quay của phép quay tâm O.
- Phép quay tâm O góc α thường được kí hiệu là Q(O,α)
- Hình minh họa phép quay:
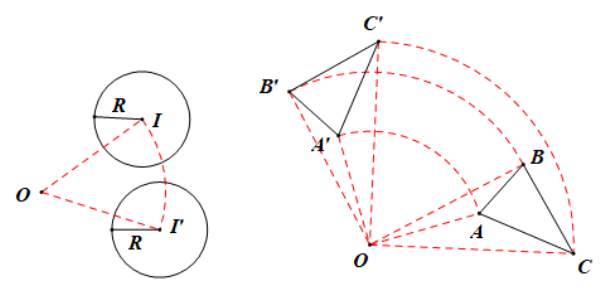
Tính chất:
- Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
- Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
Giải dạng toán quỹ tích bằng phép biến hình lớp 11
Dưới đây là hướng dẫn minh họa cách giải toán quỹ tích bằng phép biến hình lớp 11.
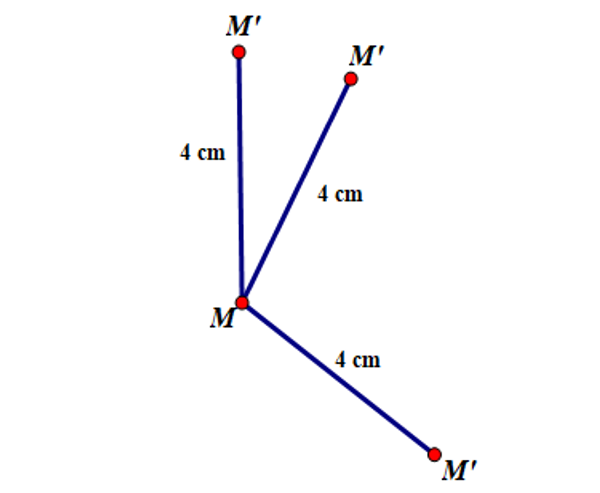
Bài tập: Cho trước số a dương, với mỗi điểm M trong mặt phẳng, gọi M’ là điểm sao cho MM’ = a. Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên có phải là một phép biến hình không?
Hướng dẫn: Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên không phải là một phép biến hình vì M’ không phải là điểm duy nhất được xác định trên mặt phẳng. Ví dụ: a = 4 cm
Tham khảo ngay các khoá học online của Marathon Education
Phép biến hình lớp 11 là phần kiến thức quan trọng trong chương trình phổ thông vì có nhiều ứng dụng vào mảng hình học không gian. Qua bài viết trên, Team Marathon Education hy vọng đã giúp các em củng cố kiến thức và tự tin hoàn thành các bài tập liên quan phép biến hình dễ dàng. Các em có thể học online các nội dung bài học Toán – Lý – Hoá hữu ích khác tại website của Marathon Education. Chúc các em học tập ngày một tiến bộ!






