Công Thức Tính Nguyên Hàm e Mũ u Và Các Hàm Số Đơn Giản

Ở chương trình Toán đại số lớp 12, kiến thức về nguyên hàm e mũ u và các hàm số đơn giản đóng vai trò trọng điểm trong các kỳ thi. Để tìm hiểu sâu hơn về nội dung này, các em hãy đọc ngay bài viết dưới đây từ Marathon Education.

>>> Xem thêm: Toán 12 Nguyên Hàm – Lý Thuyết Và Một Số Bài Tập Ví Dụ

Lý thuyết nguyên hàm

Định nghĩa nguyên hàm

Ta có: ký hiệu K là đoạn, nửa khoảng hoặc khoảng của tập R. 

Cho hàm số f(x) đã được xác định trên K, nếu F’(x) = f(x) với mọi giá trị x ∈ K, ta có thể khẳng định rằng F(x) được gọi là nguyên hàm của hàm số f(x).

Một số định lý về nguyên hàm:

• Trong trường hợp F(x) được xác định là một nguyên hàm của hàm số f(x) trên tập K thì với hằng số C bất kỳ, ta đều có: G(x) = F(x)+C cũng được xem là một nguyên hàm của hàm số f(x) trên K.
• Ngược lại, nếu F(x) được xác định là một nguyên hàm của hàm số f(x) trên K thì tất cả các nguyên hàm của hàm số f(x) trên tập K để có thể được viết dưới dạng F(x) + C (với giá trị C là một hằng số bất kỳ). Ta có, ký hiệu họ nguyên hàm của hàm số f(x) là ∫f(x)dx. Theo đó, ∫f(x)dx =F(x) + C, C ∈ R.

Tính chất của nguyên hàm

Liên quan đến định nghĩa cũng như định lý về nguyên hàm, các em cũng cần phải ghi nhớ một số tính chất quan trọng như sau:

• ∫f(x)dx = F(x) + C, C ∈ R.
• ∫kf(x)dx = k ∫f(x)dx (với k là hằng số khác 0)
• ∫(f(x) ± g(x)) = ∫f(x)dx ± ∫g(x)dx.

Lý thuyết hàm số mũ

Trước khi đi vào phần lý thuyết về nguyên hàm e mũ u, các em cần phải nắm chắc một số phần kiến thức trọng tâm về hàm số mũ như sau:

Định nghĩa hàm số mũ

Hàm số mũ được định nghĩa là hàm số ở dạng y = a^x với điều kiện hệ số a luôn dương và khác giá trị 1.

Tính chất hàm số mũ

Hàm số mũ y = a^x (a>0, a1) sẽ tồn tại một số tính chất như sau:

• Hàm số mũ có tập xác định là R.
• x ∈ R, ta có đạo hàm của hàm số mũ y = a^x sẽ là y′ = a^xlna.
• Xét về chiều biến thiên của hàm số mũ, ta có:
  • Nếu a > 1 thì hàm số sẽ luôn đồng biến.
  • Trường hợp 0 < a < 1 thì hàm số sẽ luôn nghịch biến.
• Trục Ox sẽ là đường tiệm cận ngang của đồ thị. 
• Đồ thị sẽ nằm hoàn toàn phía trên của trục hoành (y = a^x > 0 ∀x). Đồng thời, đồ thị hàm số mũ sẽ luôn cắt trục tung tại điểm (0;1) và đi qua điểm (1;a).

>>> Xem thêm: Lý Thuyết Và Đồ Thị Của Hàm Số Mũ, Hàm Số Lôgarit

Hằng số e trong toán học là gì?

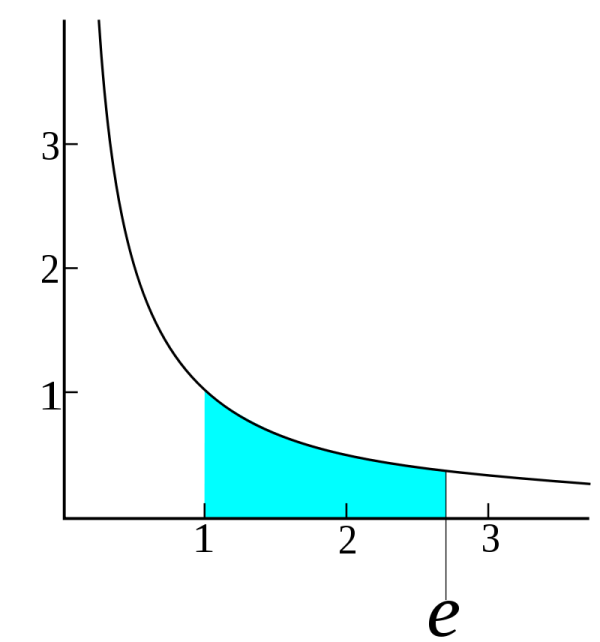
Số e là một hằng số toán học có giá trị gần bằng với 2,71828… Hằng số này có thể được biểu diễn ở nhiều cách khác nhau. Cụ thể:

\begin{aligned}
&\footnotesize\bull\text{Số e là số thực dương duy nhất mà giá trị của đạo hàm của hàm số mũ cơ số }\\
&\footnotesize\text{e cũng chính bằng hàm số đó: }\frac{d}{dt}e^t=e^t.\\
&\footnotesize\bull\text{Số e là số thực dương duy nhất mà } \frac{d}{dt}log_et=\frac{1}{t}.\\
&\footnotesize\bull\text{Số e là giới hạn của }(1 + \frac{1}{n})^n \text{ khi n tiến về vô cực là }e = \lim\limits_{n \to \infin}(1 + \frac{1}{n})^n.\\
&\footnotesize\bull\text{Số e cũng là tổng của chuỗi vô hạn trong đó n! là giai thừa của n: }\\
&\footnotesize\sum^e_{n=0}\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+ \frac{1}{2!}+\frac{1}{3!}+...\\
&\footnotesize\bull\text{Số e là số thực dương duy nhất mà }\int_1^e\frac{1}{t}dt=1. \text{ Nghĩa là diện tích hình }\\
&\footnotesize\text{phẳng được giới hạn bởi đồ thị hàm số }y=\frac{1}{t} \text{từ t = 1 đến t = e sẽ có diện }\\
&\footnotesize\text{tích bằng 1.}
\end{aligned}

Bảng các công thức tính nguyên hàm e mũ u

Để tính được nguyên hàm e mũ u, các em có thể áp dụng một số công thức nguyên hàm thông qua các bảng nguyên hàm e mũ u cơ bản và kết hợp như sau:

Bảng nguyên hàm e mũ cơ bản

\begin{aligned}
\hline
\begin{array}{|cc|}
&1. \int e^xdx=e^x+C\\ \hline
&2. \int e^udu=e^u+C \\ \hline
&3. \int e^{ax+b}dx=e^{ax+b}+C \\ \hline
&4. \int e^{-x}dx=-e^{-x}+C \\ \hline
&5. \int e^{-u}dx=-e^{-u}+C \\ \hline
\end{array}
\end{aligned}

Bảng nguyên hàm e mũ kết hợp

\def\arraystretch{1.5}
\begin{aligned}
\hline
\begin{array}{|cc|}
&6. \int cos(ax).e^{bx}=\frac{(asin(ax)+bcos(ax)).e^{bx}}{a^2+b^2}+C\\ \hline
&7. \int cos(au).e^{bu}=\frac{(bsin(au)-acos(au)).e^{bu}}{a^2+b^2}+C\\ \hline
&8. \int e^{au}du=\frac{e^{au}}{a}+C \\ \hline
&9. \int u.e^{au}du=(\frac{u}{a}-\frac{1}{a^2})e^{au}+C \\ \hline
&10. \int u^ne^{au}du=\frac{u^ne^{au}}{a}-\frac{n}{a} \int u^{n-1}e^{au}du+C
\\\hline
\end{array}
\end{aligned}

>>> Xem thêm: Tính Nguyên Hàm Ln x. Bài Tập Vận Dụng Có Lời Giải Chi Tiết

Tham khảo ngay các khoá học online của Marathon Education

Trên đây là các thông tin liên quan đến nguyên hàm e mũ u và các hàm số đơn giản. Hy vọng qua bài viết này, các em sẽ “bỏ túi” được nhiều kiến thức bổ ích và mới mẻ. 

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!