Cách Tính Đạo Hàm Cos2x Và Bài Tập Vận Dụng Có Đáp Án
Trong bài viết này, Marathon Education sẽ chia sẻ đến các em lý thuyết về đạo hàm lượng giác cùng với cách tính đạo hàm cos2x một cách nhanh chóng và chính xác. Nội dung bài viết đã được Marathon Education biên soạn đầy đủ và chính xác để hỗ trợ các em học tốt hơn. Để hiểu rõ và nắm vững công thức đạo hàm cos2x, các em hãy đọc kỹ bài viết và vận dụng lý thuyết làm bài tập nhiều lần cho thuần thục.
>>> Xem thêm: Đạo Hàm Là Gì? Các Công Thức Tính Đạo Hàm Thường Gặp
Đạo hàm của hàm số lượng giác
- Đạo hàm của một hàm số mô tả sự biến thiên của hàm số tại một điểm nào đó.
- Đạo hàm của một hàm số lượng giác là phương pháp toán học tìm tốc độ biến thiên của hàm số lượng giác theo sự biến thiên của biến số.
- Các hàm số lượng giác thường gặp bao gồm sin(x), cos(x), tan(x) và cotg(x):
\begin{aligned}
&\footnotesize \circ \text{Hàm số y = sinx có đạo hàm }\forall x\in\R \text{ và }(sinx)'=cosx.\\
&\footnotesize \circ \text{Hàm số y = cosx có đạo hàm }\forall x\in\R \text{ và }(cosx)'=-sinx.\\
&\footnotesize \circ \text{Hàm số y = tanx có đạo hàm }\forall x\not=\frac{\pi}{2}+k\pi,\ k\in \R \text{ và }(tanx)'=\frac{1}{cos^2x}.\\
&\footnotesize\circ \text{Hàm số y = cotx có đạo hàm }\forall x\not=k\pi,\ k\in \R \text{ và }(cotx)'=-\frac{1}{sin^2x}.\\
\end{aligned}
Bảng tổng hợp đạo hàm của hàm số lượng giác cơ bản và hàm số lượng giác ngược
Đầu tiên, các em hãy tham khảo và học thuộc bảng tổng hợp hàm số lượng giác cơ bản và hàm số lượng giác ngược dưới đây:

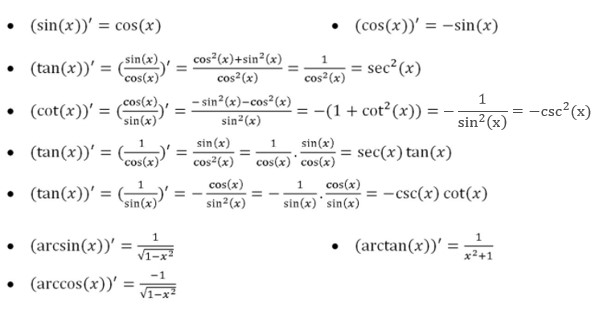
Đạo hàm của y = cosx
Từ lý thuyết về đạo hàm lượng giác, các em có thể kết luận:
Hàm số y = cosx có đạo hàm x R và (cosx)’= – sinx.
Cách tính đạo hàm cos2x
Các em thực hiện tìm đạo hàm cos2x theo hướng dẫn:
Ta tính đạo hàm y = cos2x bằng cách áp dụng công thức (cosu)’ = – u’.sinu.
Ta có: y’ = (cos2x)’ = – (2x)’.sin2x = -2sin2x
>>> Xem thêm: Cách Tìm Đạo Hàm Sin2x. Bài Tập Vận Dụng Có Đáp Án
Bài tập vận dụng về đạo hàm cos2x
Các em cùng luyện tập các bài tập sau đây để hiểu rõ và nhớ lâu hơn công thức đạo hàm cos2x. Mỗi dạng bài tập dưới sẽ có cách thực hiện khác nhau, khi áp dụng lý thuyết tuỳ vào dạng bài tập mà các em linh hoạt vận dụng các kiến thức để giải bài cho chính xác.
Bài tập 1:
\text{Tính đạo hàm của hàm số: }y = tan(2x+1) - xcos2x.
Hướng dẫn:
\begin{aligned}
y'&=\frac{(2x+1)'}{cos^2(2x+1)}-[x'.cos2x+x.(cos2x)']\\
&=\frac{2}{cos^2(2x+1)}-cos2x-2xsin2x
\end{aligned}
Bài tập 2:
\text{Cho hàm số }f(x) = cos2x.\text{ Tính giá trị của }f'(\frac{π}{6}).
Hướng dẫn:
\text{Các em tính đạo hàm của }f(x) = cos2x \text{ sau đó thế giá trị }x = \frac{π}{6} \text{ vào công thức }f’(x).
Ta có:
\begin{aligned}
&f'(x)=(cos2x)'=(2x)'(-sin2x)=-2sin2x\\
&f'\left(\frac{\pi}{6}\right)=-2sin\frac{2\pi}{6}=-2sin\frac{\pi}{3}=-\sqrt3
\end{aligned}
Bài tập 3: Tìm đạo hàm cấp hai của hàm số y = cos2x.
Hướng dẫn:
y’ = (cos2x)’= -2sin2x
y’’ = (-2.sin2x)’ = (-2)’.sin2x + (-2).(sin2x)’= -2.(2x)’.cos2x = -4cos2x
Bài tập 4: Tìm đạo hàm của hàm số y = cos22x
Hướng dẫn:
y’ = (cos22x)’ = 2.(cos2x)’.cos2x = -4.sin2x.cos2x = -2sin4x
Bài tập 5:
Tính \ đạo \ hàm \ của \ hàm \ số \ y =\frac{sin2x+cos2x}{2sin2x - cos2x}
Hướng dẫn:
\begin{aligned}
y'&=\frac{(sin2x+cos2x)'.(2sin2x - cos2x)-(2sin2x - cos2x)'.(sin2x+cos2x)}{(2sin2x - cos2x)^2}
\\
&=\frac{(cos2x-sin2x).(2sin2x - cos2x)-(4cos2x+2sin2x).(sin2x+cos2x)}{(2sin2x - cos2x)^2}
\\
&=\frac{-6cos^22x-6sin^22x}{(2sin2x - cos2x)^2}
\\
&=\frac{-6}{(2sin2x - cos2x)^2}
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Trên đây là toàn bộ nội dung liên quan đến cách tính và công thức đạo hàm cos2x. Với phần lý thuyết và bài tập vận dụng, Marathon Education hy vọng các em hiểu bài và làm bài tập trên lớp và trong bài thi liên quan đến đạo hàm cos2x thật tốt. Các em có thể học online các nội dung bổ ích khác của môn Toán – Lý – Hoá tại website Marathon Education. Chúc các em học tập tiến bộ mỗi ngày!






