Bài tập cách tính đạo hàm tanx | Marathon Education
Cùng với nguyên hàm, đạo hàm là một chủ đề quan trọng trong chương trình Toán cấp 3. Do đó, việc nắm vững các lý thuyết về đạo hàm sẽ giúp các em vận dụng làm bài tập một cách nhanh chóng và hiệu quả hơn. Vậy có những đạo hàm lượng giác nào? Cách tính đạo hàm tanx như thế nào? Trong bài viết này, Marathon Education sẽ hướng dẫn các em cách tính đạo hàm tanx với các bài tập vận dụng cụ thể, giúp các em nắm vững kiến thức này.
Đạo hàm là gì?
Xét hàm số y = f(x) xác định trên khoảng (a;b) và điểm x0 thuộc (a;b).
\begin{aligned}
&\footnotesize\text{Nếu tồn tại một giới hạn (hữu hạn) }\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0} \text{ thì giới hạn đó được gọi là đạo hàm của hàm số }\\
&\footnotesize\text{y= f(x) tại điểm }x_0, \text{ kí hiệu là }y’(x_0) \text{ hoặc } f’(x_0).\\
&f'(x_0)=\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}
\end{aligned}
Bảng tổng hợp công thức đạo hàm lượng giác
Bảng công thức đạo hàm lượng giác cơ bản
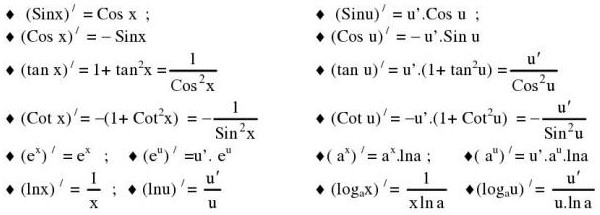
Bảng đạo hàm các hàm lượng giác ngược
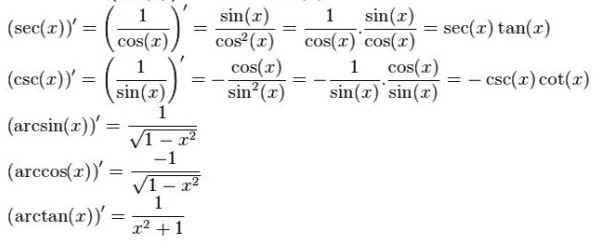
>>> Xem thêm: Công Thức Tính Đạo Hàm Lượng Giác. Bài Tập Minh Họa Có Đáp Án
Cách tính đạo hàm tanx
\begin{aligned}
&\small\text{Hàm số y = tanx có đạo hàm }\forall x\not=\frac{\pi}{2}+k\pi. \textbf{ Đạo hàm tanx }\text{được tính bằng công thức sau:}
\\
&y = (tanx)'=\frac{1}{cos^2x}=sec^2x
\\
&\small\text{Chứng minh } \textbf{đạo hàm tanx:}
\\
&y = (tanx)'=\left(\frac{sinx}{cosx}\right)'=\frac{(sin x)'.cosx-(cosx)'.sinx}{cos^2x}
\\
& \ = \frac{cos^2x+sin^2x}{cos^2x}=\frac{1}{cos^2x}=sec^2x
\\
&\small\text{Trong công thức trên ta áp dụng 3 công thức đạo hàm lượng giác cơ bản:}
\\
&cos^2x+sin^2x = 1
\\
&(sinx)'=cosx
\\
&(cosx)'=-sinx
\end{aligned}
Bài tập vận dụng
Dưới đây là một vài bài tập ứng dụng về đạo hàm tanx mà các em có thể tham khảo và luyện tập.
Bài tập 1: Tìm đạo hàm của hàm số:
y= tan (4x+ 1) \ – \ cot 2x
Cách giải:
\begin{aligned}
y'&=[tan(4x+1)]'-(cot2x)'=\frac{(4x+1)'}{cos^2(4x+1)}+\frac{(2x)'}{sin^22x}\\
&=\frac{4}{cos^2(4x+1)}+\frac{2}{sin^22x}
\end{aligned}
Bài tập 2: Tìm đạo hàm của hàm số sau:
y = sin (x^2 – 3x) – tan (x^2 – 1)
Cách giải:
\begin{aligned}
y'&=[sin(x^2-3x)]'-[tan(x^2-1)]'\\
&=cos(x^2-3x)(x^2-3x)'-\frac{1}{cos^2(x^2-1)}(x^2-1)'\\
&=cos(x^2-3x)(2x-3)-\frac{2x}{cos^2(x^2-1)}
\end{aligned}
Bài tập 3: Tìm đạo hàm của hàm số sau:
y = tan \left(\sqrt{x^2 + 2x}\right)
Cách giải:
Áp dụng công thức đạo hàm tanx của hàm số hợp
\begin{aligned}
y'&=\left[tan\left(\sqrt{x^2 + 2x}\right)\right]'\\
&=\frac{1}{cos^2\left(\sqrt{x^2 + 2x}\right)}\left(\sqrt{x^2 + 2x}\right)'\\
&=\frac{1}{cos^2\left(\sqrt{x^2 + 2x}\right)}.\frac{1}{2\sqrt{x^2 + 2x}}.(x^2+2x)'\\
&=\frac{1}{cos^2\left(\sqrt{x^2 + 2x}\right)}.\frac{1}{2\sqrt{x^2 + 2x}}.(2x+2)\\
&=\frac{x+1}{cos^2\left(\sqrt{x^2 + 2x}\right).\sqrt{x^2 + 2x}}
\end{aligned}
Bài tập 4: Tìm đạo hàm của hàm số sau:
y = (1 + tanx)^4
Cách giải:
Áp dụng công thức đạo hàm của hàm hợp y = un với u là 1 + tanx.
Ta được:
\begin{aligned}
y'&=4(1+tanx)^3(1+tanx)\\
&=4(1+tanx)^3.\frac{1}{cos^2x}\\
&=\frac{4(1+tanx)^3}{cos^2x}
\end{aligned}
Bài tập 5: Tìm đạo hàm của hàm số sau:
y = tan^2(\frac{x}{2})
Cách giải:
\begin{aligned}
&\bull\text{Áp dụng công thức đạo hàm hàm hợp} \ (u^n)'=n.u'.u^n-1
\\
&\bull\text{Áp dụng công thức đạo hàm của hàm } \ (tan u)'=\frac{u'}{cos^2u}
\end{aligned}
\begin{aligned}
y'&=\left(tan^2\frac{x}{2}\right)'
\\
&=2tan\frac{x}{2}.\left(tan\frac{x}{2}\right)'
\\
&=2tan\frac{x}{2}.\frac{\left(\frac{x}{2}\right)'}{cos^2\frac{x}{2}}
\\
&=2tan\frac{x}{2}.\frac{\frac{1}{2}}{cos^2\frac{x}{2}}
\\
&=\frac{sin\frac{x}{2}}{cos\frac{x}{2}}.\frac{1}{cos^2\frac{x}{2}}
\\
&=\frac{sin\frac{x}{2}}{cos^3\frac{x}{2}}
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Các công thức đạo hàm lượng giác nói chung và đạo hàm tanx nói riêng tuy phức tạp nhưng nếu biết cách ôn luyện, các em sẽ dễ dàng nắm được lý thuyết và vận dụng vào bài tập một cách hiệu quả. Qua bài viết này, Marathon Education hy vọng các em có cái thể nắm rõ cách tính đạo hàm tanx để giải quyết dạng bài tập liên liên quan nhanh chóng.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






