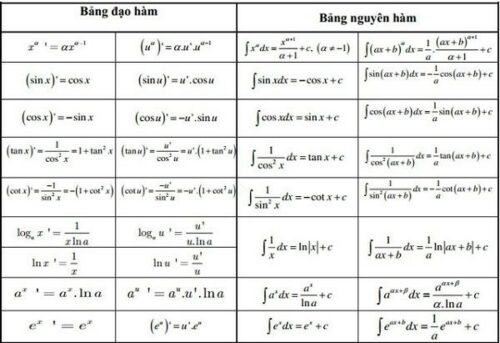
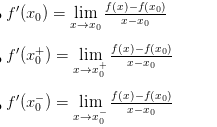Công thức đạo hàm log, logarit, căn bậc 3, căn x, lượng giác
Hàm số logarit và công thức tính đạo hàm log là những nội dung mà các em sẽ được học trong chương trình Toán 12. Đây là những kiến thức trọng tâm và xuất hiện nhiều trong các đề thi. Vì thế, trong bài viết sau, Marathon Education sẽ hệ thống lại những kiến thức cơ bản liên quan đến hàm logarit, công thức tính đạo hàm log và những ví dụ minh họa để giúp các em nắm chắc phần kiến thức này.
1.Tổng hợp các công thức đạo hàm

Quy tắc cơ bản của đạo hàm
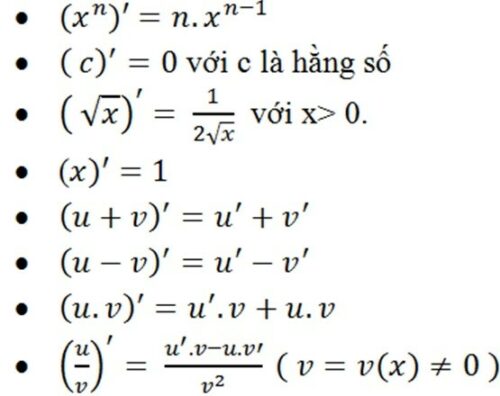
2. Bảng đạo hàm lượng giác

3. Công thức đạo hàm logarit

4. Công thức đạo hàm số mũ
5. Công thức đạo hàm log
6. Bảng đạo hàm và nguyên hàm
7. Các dạng bài toán về công thức đạo hàm
7.1 Tính đạo hàm bằng định nghĩa
Hàm số y = f(x) có đạo hàm tại điểm x= x <=> f'(x )=f'(x )
Hàm số y = f(x) có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.
Ví dụ 1: f(x) = 2x +1 tại x=2
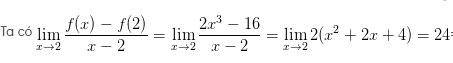
7. 2 Chứng minh các đẳng thức về đạo hàm
Ví dụ 1: Cho y = e .sinx, chứng minh hệ thức y”+2y′+ 2y = 0
Bài giải :
Ta có y′=−e .sinx + e .cosx
y′ =−e .sinx+e−x.cosx
y”=e .sinx−e .cosx−e .cosx−e .sinx = −2e .cosx
Vậy y”+ 2y′+ 2y = −2.e .cosx− −2.e .sinx + 2.e .cosx + 2.e .sinx =0
7.3 Viết phương trình tiếp tuyến khi biết tiếp điểm
Phương trình tiếp tuyến của đường cong (C): y= f(x) tại tiếp điểm M( x ;y ) có dạng:
Ví dụ: Cho hàm số y= x +3mx + ( m+1)x + 1 (1), m là tham số thực. Tìm các giá trị của
m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x = -1 đi qua điểm A(
1;2).
Tập xác định D = R
y’ = f'(x)= 3x + 6mx + m + 1
Với x = -1 => y = 2m -1, f'( -1) = -5m + 4
Phương trình tiếp tuyến tại điểm M( -1; 2m – 1) : y= ( -5m + 4 ) ( x+1) + 2m -1 (d)
Ta có A ( 1;2) ∈ (d) <=> ( -5m + 4).2 + 2m – 1 = 2 => m = 5/8
7.4 Viết phương trình tiếp khi biết hệ số góc
Viết PTTT Δ của ( C ) : y = f( x ), biết Δ có hệ số góc k cho trước
Gọi M( x ;y ) là tiếp điểm. Tính y’ => y'(x )
Do phương trình tiếp tuyến Δ có hệ số góc k => y’ = ( x ) = k (i)
Giải (i) tìm được x => y = f(x ) => Δ : y = k (x – x )+ y
Lưu ý:Hệ số góc k = y'( x ) của tiếp tuyến Δ thường cho gián tiếp như sau:
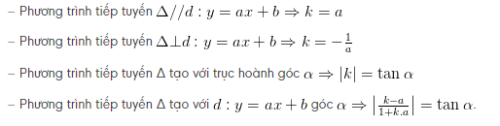
Ví dụ: Cho hàm số y=x +3x -9x+5 ( C). Trong tất cả các tiếp tuyến của đồ thị ( C ), hãy
tìm tiếp tuyến có hệ số góc nhỏ nhất.
Ta có y’ = f'( x ) = 3x + 6x – 9
Gọi x là hoành độ tiếp điểm của tiếp tuyến, vậy f'( x ) = 3 x + 6 x – 9
Ta có 3 x + 6 x – 9 =3 ( x + 2x +1) – 12 = 3 (x +1) – 12 > – 12
Vậy min f( x )= – 12 tại x = -1 => y =16
Suy ra phương trình tiếp tuyến cần tìm: y= -12( x+1)+16 <=> y= -12x + 4
7.5 Phương trình và bất phương trình có đạo hàm

Tham khảo ngay các khoá học online của Marathon Education
Team Marathon Education vừa chia sẻ cho các em những kiến thức quan trọng về hàm số logarit cũng như công thức tính đạo hàm log. Hy vọng rằng bài viết này có thể trang bị cho các em những kiến thức nền tảng cần thiết để giúp các em học Toán tốt hơn và dành được điểm cao trong các kỳ thi sắp tới. Để học trực tuyến online nhiều nội dung khác, các em đừng quên theo dõi Marathon mỗi ngày. Chúc các em thành công!