Các tính chất và cách tìm số phức liên hợp là gì?
Số phức là một trong những nội dung quan trọng trong phần Đại số lớp 12 và thường xuất hiện trong đề thi đại học. Vậy số phức là gì? Số phức liên hợp là gì? Cách tìm số phức liên hợp như thế nào? Trong bài viết này, Marathon Education sẽ giúp các em củng cố những lý thuyêt liên quan bao gồm khái niệm, các tính chất và hướng dẫn các em giải một số bài tập cơ bản.
>>> Xem thêm:
Số Phức Đối Là Gì? Cách Tìm Điểm Biểu Diễn Của Số Phức Đối
Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10
Số phức là gì?
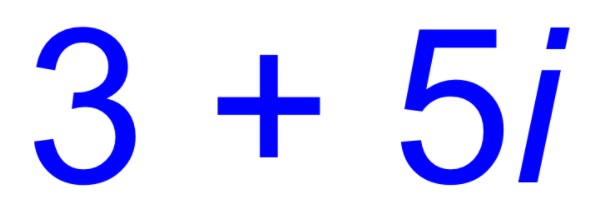
Các phương trình bậc hai như x2 + 1 = 0 không có nghiệm thực, vì x2 không thể bằng -1. Với mong muốn mở rộng tập hợp số thực để mọi phương trình bậc n đều có nghiệm, người ta đã đưa ra khái niệm số phức. Đơn vị ảo của số phức có kí hiệu là i và là nghiệm của phương trình i2 = -1.
Vậy, số phức (tên tiếng Anh là complex number) là số có dạng z = a + bi. Trong đó a và b là các số thực, còn i là đơn vị ảo với i2 = -1. Đồng thời, a được gọi là phần thực, b là phần ảo, i là đơn vị ảo.
Tập hợp các số phức ký hiệu là C.
Ví dụ:
Số phức 6 + 8i có phần thực là 6, phần ảo là 8.
Số phức 5 – 9i cóphần thực là 5, phần ảo là -9.
Số phức -7 – i, có phần thực là -7, phần ảo là -1.
Số phức có thể được biểu diễn trên mặt phẳng phức. Trục hoành là trục số thực và trục tung là trục số ảo. Do đó, một số phức được xác định bằng một điểm có tọa độ (a,b). Một số phức nếu có phần thực bằng không thì gọi là số thuần ảo (số ảo). Nếu số phức đó có phần ảo bằng không thì trở thành số thực R. Việc mở rộng trường số phức giúp chúng ta giải những bài toán không thể giải trong trường số thực.
>>> Xem thêm: Tổng Hợp Các Kí Hiệu Trong Toán Học Phổ Biến Đầy Đủ Và Chi Tiết
Số phức liên hợp là gì?
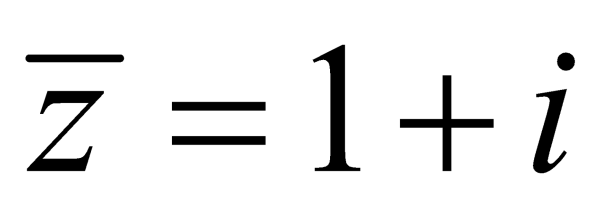
Theo như định nghĩa về số phức ở trên, số phức có dạng a + bi với i2 = -1.
\begin{aligned}
&\textbf{Số phức liên hợp }\text{chính là a – bi và được ký hiệu là } \overline{z}, \text{ với }\overline{z} = a - bi.\\
&\text{Ví dụ: ta có: z = 2 + 3i, vậy số phức liên hợp của z là } \overline{z}= 2 – 3i.
\end{aligned}
Các tính chất của số phức liên hợp
Số phức liên hợp có một số tính chất như sau:
|z| = |\overline{z}|; ∀z∈\Complex
\small \text{Do đó, 2 điểm biểu diễn của z và } \overline{z} \text{ sẽ đối xứng với nhau qua trục Oxy trên mặt phẳng tọa độ Oxy.}
\overline{z+z'}=\overline{z}+\overline{z'}
Theo công thức này, liên hợp của một tổng sẽ bằng tổng các số phức liên hợp. Công thức trên còn đúng với cả phép trừ, phép nhân và phép chia.
z . \overline{z} = a^2 + b^2
Đây là công thức quan trọng và thường được áp dụng nhiều trong các bài toán.
\begin{aligned}
&\text{Với z là số thực, thì ta có trong mọi trường hợp } z = \overline{z}\\
&\text{Với z là số ảo tức là phần thực của nó = 0 thì }z = –\overline{z}
\end{aligned}
Cách tìm số phức liên hợp
\text{Cho số phức z = a + bi. Ta gọi }\textbf{số phức liên hợp }\text{của số phức z = a + bi là }\overline{z} = a - bi.
Kết quả: ∀ z ∈ C ta có:
\begin{aligned}
&\bull |z| = |\overline{z}|\\
&\bull \overline{z_1\pm z_2}=\overline{z_1}\pm\overline{z_2}\\
&\bull \overline{z_1.z_2}=\overline{z_1}.\overline{z_2}\\
&\bull \overline{\left(\frac{z_1}{z_2}\right)}=\frac{\overline{z_1}}{\overline{z_2}}\\
&\bull \text{z là số thực khi }z = \overline{z}\\
&\bull \text{z là số thuần ảo khi }z = - \overline{z}
\end{aligned}
Bài tập vận dụng về số phức liên hợp
Để giúp các em nắm vững hơn kiến thức về số phức liên hợp, Team Marathon Education đã tổng hợp một số bài tập vận dụng và hướng dẫn giải chi tiết sau:
Bài tập 1:
\text{Cho số phức }z = 1 + 3i .\text{ Tìm số phức }\overline{z}.
Cách giải:
z = 1 + 3i \Rightarrow \overline{z} = 1 - 3i
Bài tập 2:
Tìm số phức liên hợp của các số phức sau:
a. z = -3 + 5i
b. z = 3 – 4i
c. z = 5 – 3i
d. z = i(3i +1)
Cách giải:
\begin{aligned}
&\text{a. Số phức liên hợp của z = -3 + 5i là } \overline{z}=-3-5i\\
&\text{b. Số phức liên hợp của z = 3 - 4i là } \overline{z}=3+4i\\
&\text{c. Số phức liên hợp của z = 5 - 3i là } \overline{z}=5+3i\\
&\text{d. Ta có về dạng cơ bản: z = i(3i + 1) = -3 + i}\\
&\text{Vậy số phức liên hợp của z = -3 + i là } \overline{z}=-3-i\\
\end{aligned}
Bài tập 3
\text{Tìm số phức liên hợp của số phức }z=\frac{1+i}{2-i}.
Cách giải:
\begin{aligned}
&\frac{1+i}{2-i}=\frac{(1+i)(2+i)}{(2-i)(2+i)}=\frac{1+3i}{2^2-i^2}=\frac15+\frac35i\\
&\Rightarrow \overline{z}=\frac15-\frac35i
\end{aligned}
Bài tập 4:
\text{Tìm số phức z thỏa mãn }z - (2 + 3i)\overline{z} = 1 - 9i .
Cách giải:
\begin{aligned}
&\text{Gọi }z = a + bi => \overline{z}=a-bi\\
&z - (2 + 3i)\overline{z} = 1 - 9i\\
&\Leftrightarrow (a+bi)-(2+3i)(a-bi)=1-9i\\
&\Leftrightarrow a + bi -2a+2bi-3ai+3b.i^2=1-9i\\
&\Leftrightarrow a+ bi - 2a + 2bi - 3ai - 3b = 1 - 9i\\
&\Leftrightarrow -a-3b+(b+2b-3a)i=1-9i\\
&\Leftrightarrow \begin{cases} -a-3b=1\\-3a+3b=-9\end{cases}\\
&\Leftrightarrow \begin{cases} a=2 \\b=-1\end{cases}\\
&\text{Vậy }z = 2 - i
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Với kiến thức đã chia sẻ trong bài viết, Team Marathon Education hy vọng đã giúp các em nắm vững kiến thức về số phức, số phức liên hợp bao gồm khái niệm, tính chất, cách tìm và ví dụ minh họa để giải quyết tốt các bài tập trong kỳ thi sắp đến.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






