Lý Thuyết Toán 10 Các Phép Toán Tập Hợp
Toán 10 các phép toán tập hợp là một trong những phần kiến thức mà các em cần nắm khi học về bộ môn này. Bài viết dưới đây của Team Marathon Education sẽ giúp các em nắm vững được nội dung này và cách giải bài tập chính xác.
>>> Xem thêm: Lý Thuyết Toán 10 Mệnh Đề Và Các Dạng Mệnh Đề Thường Gặp
>>> Xem thêm: Học Toán lớp 10 Online Hiệu Quả Cùng Marathon Education
Định nghĩa tập hợp
Đây là phần lý thuyết quan trọng khi nhắc đến Toán 10 các phép toán tập hợp. Vì vậy, các em hãy dành thời gian chú ý theo dõi:
Tập hợp là gì?
Tập hợp (hay còn gọi là tập) là một khái niệm cơ bản trong toán học.
Giả sử ta có tập hợp A.
- a ∈ A: a là một phần tử của tập hợp A (đọc là a thuộc A).
- a ∉ A: a không phải là một phần tử của tập hợp A (đọc là a không thuộc A).
Cách xác định tập hợp
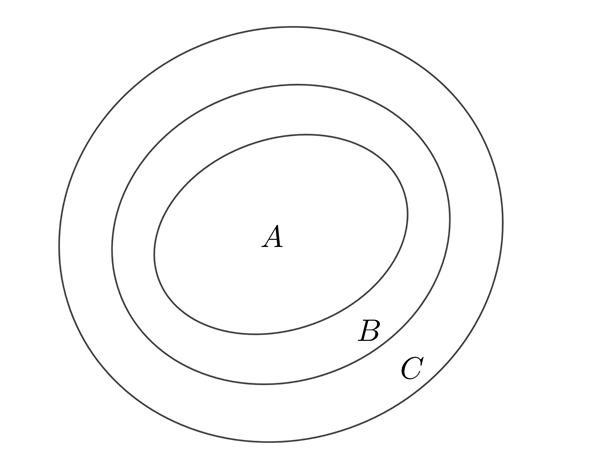
Một tập hợp có thể được xác định bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó.
Các em có thể xác định một tập hợp bằng một trong hai cách sau:
- Liệt kê các phần tử của nó.
- Chỉ ra tính chất đặc trưng cho các phần tử của nó.
Tập hợp thường được minh hoạ bằng một hình phẳng bao quanh bởi một đường kín, gọi là biểu đồ Ven.
Tập hợp rỗng
Tập hợp rỗng là tập hợp không chứa phần tử nào, kí hiệu là ø.
Nếu A không phải là tập hợp rỗng thì A chứa ít nhất một phần tử.
A ≠ ø ⇔ ∃x: x ∈ A.
Tập hợp con
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì A là một tập hợp con của B. Ta có thể viết như sau:
- A ⊂ B (đọc là A chứa trong B).
- B ⊃ A (đọc là B chứa A hoặc B bao hàm A)
Như vậy A ⊂ B (∀x: x ∈ A ⇒ x ∈ B).
Nếu A không phải là một tập con của B, ta viết A ⊄ B.
Ta có các tính chất sau :
- A ⊂ A với mọi tập hợp A.
- Nếu A ⊂ B và B ⊂ C thì A ⊂ C.
- ø ⊂ A với mọi tập hợp A.
Các phép toán tập hợp là gì?
Giao của hai tập hợp
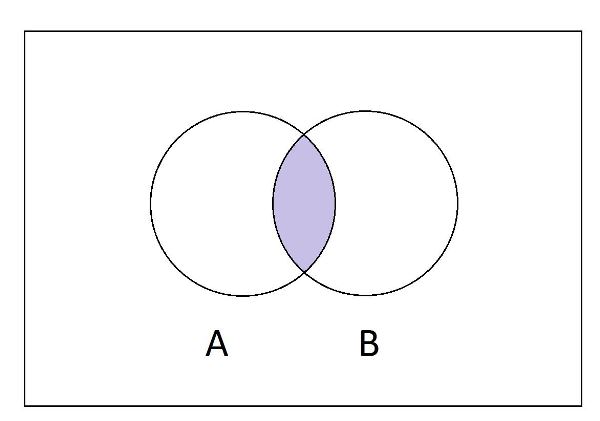
Giao của hai tập hợp A và B là tập hợp gồm các phần tử vừa thuộc A và vừa thuộc B.
Kí hiệu: A ∩ B
Ta viết: A ∩ B = {x|x ∈ A và x ∈ B}
Hợp của hai tập hợp
Hợp của hai tập hợp A và B là là tập hợp gồm các phần tử thuộc A hoặc thuộc B.
Kí hiệu: A ∪ B
Ta viết: A ∪ B = {x|x ∈ A hoặc x ∈ B}
Hiệu của hai tập hợp
Hiệu của hai tập hợp A và B là tập hợp gồm các phần tử thuộc A và không thuộc B.
Kí hiệu: A \ B
Ta viết: A \ B = {x|x ∈ A và x ∉ B}
Phần bù của hai tập hợp
Phần bù của hai tập hợp A và B là phần bù của B trong A.
Kí hiệu: CAB
Bài tập minh họa Toán 10 các phép toán tập hợp
Các em cùng theo dõi những bài tập minh hoạ để hiểu thêm về phần kiến thức Toán 10 các phép toán tập hợp.
Bài 1 SGK Đại số 10
Đề bài: Kí hiệu A là tập hợp các chữ cái trong câu “CÓ CHÍ THÌ NÊN”, B là tập hợp các chữ cái trong câu “CÓ CÔNG MÀI SẮT CÓ NGÀY NÊN KIM”. Hãy xác định A ∩ B, A ∪ B, A \ B và B \ A.
Bài giải:
Ta có:
A = {C, O, H, I, T, N, Ê }; B = {C, O, N, G, Ô, M, A, Ă, I, S, T, Y, Ê, K}
⇒ A ∩ B = {C, O, I, T, N, Ê}
⇒ A ∪ B = { C, O, Ô, N, G, M, A, Ă, I, S, T, Y, Ê, K, H}
⇒ A \ B = {H}
⇒ B \ A = {G, S, K, M, A, Ô, Ă, Y}
Bài 3 SGK Đại số 10
Đề bài:
Trong số 45 học sinh của lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa học lực giỏi, vừa có hạnh kiểm tốt. Hỏi
a) Lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải học lực giỏi hoặc có hạnh kiểm tốt?
b) Lớp 10A có bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt?
Bài giải:
a) Các bạn được HLG = 15.
Các bạn được HKT = 20.
Số bạn HLT + HKT = 10.
→ Số bạn được HKT mà không được HLG = 20 – 10 = 10.
→ Số bạn được HLG mà không được HKT = 15 – 10 = 5.
Vậy số bạn được khen thưởng = (số bạn được HKT mà không được HLG) + (số bạn được HLG mà không được HKT) + (số bạn vừa được HLG, vừa được HKT) = 5 + 10 + 10 = 25 (bạn).
b) Số học sinh chưa được xếp loại HLG và chưa có HKT là: 45 – 25 = 20 (bạn).
Tham khảo ngay các khoá học online của Marathon Education
Là những kiến thức cơ bản đầu tiên của cấp 3, các em nên ghi nhớ và nắm thật vững phần nội dung về Toán 10 các phép toán tập hợp. Ngoài ra, các em có thể tham khảo thêm các bài học trực tuyến bổ ích cho các môn Toán – Lý – Hóa tại website của Marathon Education. Chúc các em có được những giờ học thú vị!






