Tổng Hợp Công Thức Hình Học Toán 12 Đầy Đủ Và Chi Tiết Nhất

Công thức hình học về khối đa diện và hình học phẳng là kiến thức rất quan trọng trong các kỳ thi. Để chinh phục được bài tập hình học và đạt kết quả cao trong thi cử, các em cần phải thuộc lòng công thức toán hình 12. Bài viết hôm nay Marathon Education sẽ giới thiệu đến các em những công thức hình học toán 12 đầy đủ và chi tiết nhất.

>>> Xem thêm: Tổng Hợp Công Thức Toán 12 Đầy Đủ Và Chính Xác

>>> Xem thêm: Học Toán Online Livestream Bứt Phá Điểm Số Cùng Với Marathon Education

Tổng hợp công thức toán hình 12 khối đa diện

Bài tập khối đa diện là một trong những dạng bài hình học không gian phổ biến trong chương trình toán hình 12. Vì vậy, các em cần nắm vững một số công thức toán hình 12 về khối đa diện dưới đây để làm bài thật chính xác:

Công thức tính thể tích hình chóp

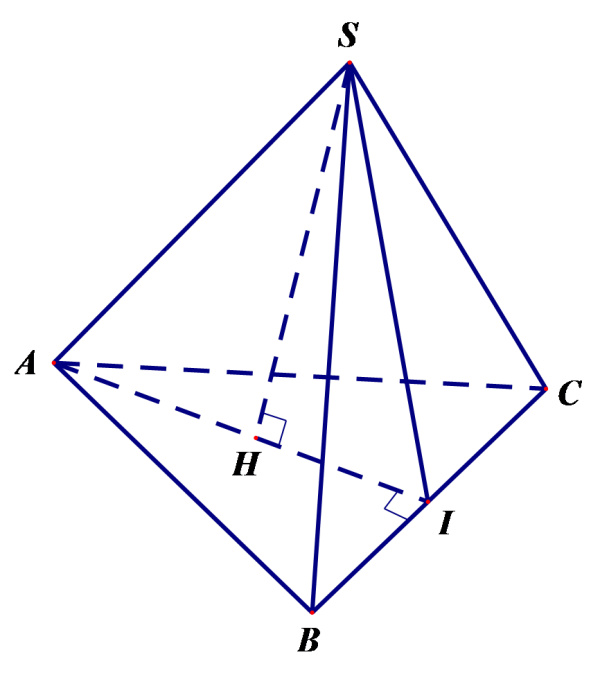
Hình chóp là một khối đa diện có mặt đáy là hình đa giác và các mặt bên được tạo thành bởi các hình tam giác có chung đỉnh. Công thức chung để tính thể tích hình chóp cụ thể như sau:

V=\frac{1}{3}.S.h

Trong đó:

• V là thể tích hình chóp
• S là diện tích mặt đáy
• h là chiều cao hình chóp

Hình tứ diện đều là một loại hình chóp đặc biệt có tất cả các mặt là tam giác đều có cạnh bằng nhau. Các em nên ghi nhớ các công thức tính hình tứ diện đều dưới đây để giải bài tập nhanh hơn:

\begin{aligned}
&\bull\text{Chiều cao: }h=\frac{a\sqrt{6}}{3}\\
&\bull\text{Thể tích: }V=\frac{a^3\sqrt2}{12}\\
&\bull\text{Diện tích toàn phần: }S_{toàn phần}=4S_{đáy}=a^2\sqrt3
\end{aligned}

Trong đó, a là độ dài các cạnh của hình tứ diện đều.

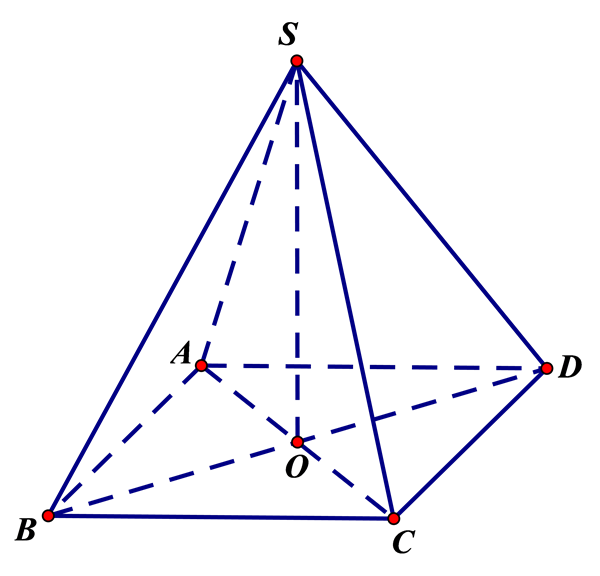
Hình chóp tứ giác đều là một loại hình chóp đặc biệt có mặt đáy là hình vuông và các mặt bên đều là tam giác cân. Dưới đây là một số công thức tính hình chóp tứ giác đều:

\begin{aligned}
&\bull\text{Thể tích: }V=\frac{1}{3}a^2h\\
&\bull\text{Diện tích toàn phần: }S_{toàn phần}=a^2+2a\sqrt{b^2-\frac{a^2}{4}}
\end{aligned}

Trong đó:

• a là độ dài cạnh đáy
• b là độ dài cạnh bên

Công thức tính thể tích hình lăng trụ

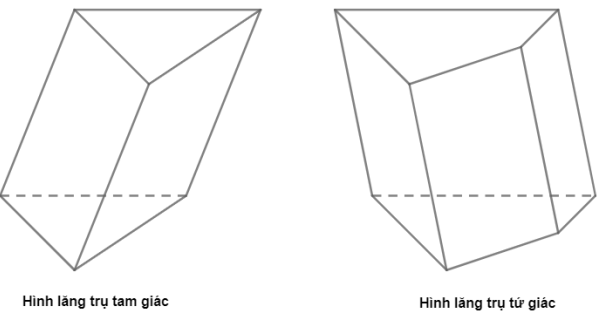
Lăng trụ là khối đa diện có 2 đáy là hình đa giác giống nhau và các mặt bên là hình bình hành. Để tính thể tích hình lăng trụ, các em dựa vào công thức sau:

V=S.h

Trong đó:

• V là thể tích hình lăng trụ
• S là diện tích mặt đáy
• h là chiều cao 

Lưu ý: Nếu là hình lăng trụ đứng thì chiều cao chính là cạnh bên.

Công thức tính thể tích hình hộp

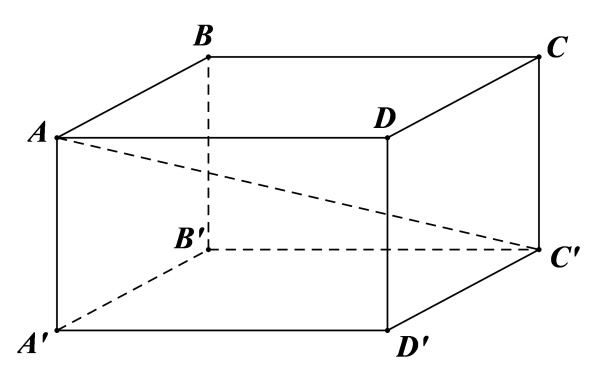
Hình hộp chữ nhật là khối hộp có 6 mặt hình chữ nhật. Để tính thể tích hình hộp chữ nhật, các em vận dụng công thức sau:

V=a.b.c

Trong đó:

• a là chiều rộng mặt đáy hình hộp chữ nhật
• b là chiều dài mặt đáy hình hộp chữ nhật
• c là chiều cao hình hộp chữ nhật

Hình lập phương là khối hộp có 6 mặt đều là hình vuông. Dưới đây là công thức tính thể tích hình lập phương đơn giản, dễ nhớ:

V=a^3

Trong đó:

• a là cạnh của các mặt khối lập phương

Công thức tính thể tích hình nón

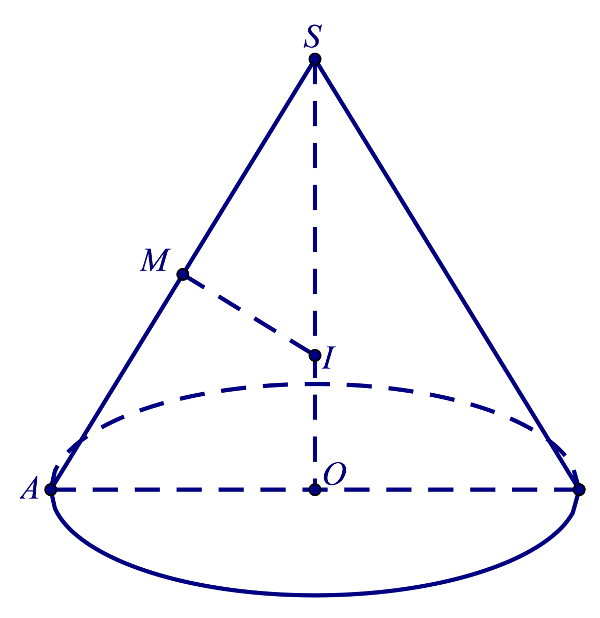
Hình nón là hình được tạo thành khi quay một tam giác vuông một vòng quanh một cạnh góc vuông. Để tính thể tích hình nón, các em hãy ghi nhớ công thức cụ thể sau:

V=\frac{1}{3}.S.h=\frac{1}{3}\pi.r^2.h

Trong đó:

• r là bán kính mặt đáy
• h là chiều cao hình nón

Công thức tính thể tích hình cầu

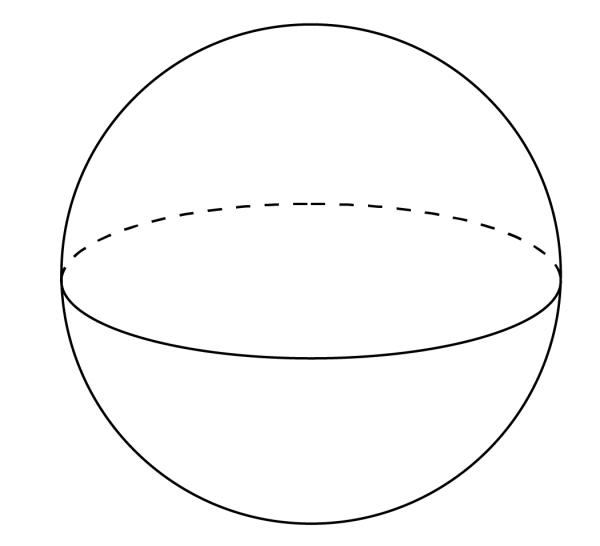
Trong các công thức toán hình 12 của khối đa diện, các em cũng nên lưu ý đến công thức tính thể tích hình cầu như sau:

V=\frac{4}{3}\pi.R^3

Trong đó:

• R là bán kính khối cầu 

Công thức tính tỉ số thể tích

Các công thức toán hình 12 cũng đề cập đến nội dung về tỉ số thể tích, cụ thể như sau:

\frac{V_{S_{A'B'C'}}}{V_{S_{ABC}}}=\frac{SA'}{SA}=\frac{SB'}{SB}=\frac{SC'}{SC}

Công thức tính một số đường đặc biệt

Ngoài ra, các em cũng cần lưu ý một số công thức toán hình 12 của một số đường đặc biệt như sau:

\begin{aligned}
&\small\bull\text{Đường chéo của hình vuông có cạnh là a thì có giá trị là }a\sqrt2.\\
&\small\bull\text{Đường chéo của hình lập phương có cạnh là a thì có giá trị là }a\sqrt3.\\
&\small\bull\text{Đường chéo của hình hộp chữ nhật có 3 kích thước a, b, c được tính theo công thức }\sqrt{a^2+b^2+c^2}.\\
&\small\bull\text{Đường cao của tam giác đều có cạnh là a thì có giá trị là }\frac{a\sqrt3}{2}.

\end{aligned}

>>> Xem thêm: Chia Sẻ Bí Quyết Học Tốt Hình Học Không Gian Lớp 11

Công thức hình phẳng

Công thức hình phẳng cũng là một kiến thức cần nắm trong những công thức toán hình 12. Nội dung của công thức hình phẳng có 2 phần, bao gồm hệ thức lượng trong tam giác và các công thức tính diện tích cho từng hình cụ thể. 

Hệ thức lượng trong tam giác

Đối với tam giác ABC vuông tại A, đường cao AH thì ta có một số hệ thức lượng như sau:

\begin{aligned}
&\bull AB^2+AC^2=B^2\\
&\bull AB^2=BH.BC\\
&\bull AC^2=CH.BC\\
&\bull AH.BC=AB.AC\\
&\bull AH^2=BH.CH\\
&\bull \frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\\
&\bull AB=BC.sinC=BC.cosB=AC.tanC=AC.cotB\\

\end{aligned}

Cho tam giác ABC có độ dài 3 cạnh lần lượt là a, b, c, độ dài đường trung tuyến là m_a, m_b, m_c, bán kính của đường tròn nội tiếp là R, bán kính đường tròn nội tiếp là r, nửa chu vi là p thì ta có các hệ thức sau:

• Định lý hàm số côsin:

a^2=b^2+c^2-2bc.cosA\\b^2=c^2+a^2-2ca.cosB\\
c^2=a^2+b^2-2ab.cosC

• Định lý hàm số sin:

\frac{a}{sinA}=\frac{b}{sinB}=\frac{C}{sinC}=2R

• Độ dài của đường trung tuyến:

\def\arraystretch{1.5}
\begin{array}{c}
m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}\\
m_b^2=\frac{c^2+a^2}{2}-\frac{b^2}{4}\\
m_c^2=\frac{a^2+b^2}{2}-\frac{c^2}{4}
\end{array}

Công thức tính diện tích

Hình tam giác:

\begin{aligned}
&\bull S=\frac{1}{2}a.h_a=\frac{1}{2}b.h_b=\frac{1}{2}c.h_c\\
&\bull S=\frac{1}{2}bc.sinA=\frac{1}{2}.ac.sinB=\frac{1}{2}.ab.sinC\\
&\bull S=\frac{abc}{4R}\\
&\bull S=pr\\
&\bull S=\sqrt{p(p-a)(p-b)(p-c)}\\
&\bull \text{ΔABC vuông tại A: }S=\frac{AB.AC}{2}=\frac{BC.AH}{2}\\
&\bull \text{ΔABC đều, cạnh a: }AH=\frac{a\sqrt3}{2},S=\frac{a^2\sqrt3}{4}\\
\end{aligned}

Hình chữ nhật:

S=ab \text{ (a, b là chiều dài và chiều rộng)}

Hình vuông:

S=a^2\text{ (a là cạnh hình vuông)}

Hình thang:

S=\frac{1}{2}(a+b)h \text{ (a, b là hai cạnh đáy và h là chiều cao)}

Tứ giác có hai đường chéo vuông góc:

S=\frac{1}{2}AC.BD \text{ (AC và BD là 2 đường chéo vuông góc của tứ giác)}

Tham khảo ngay các khoá học online của Marathon Education

Trên đây là các công thức toán hình 12 về khối đa diện và hình học phẳng quan trọng cần ghi nhớ. Hy vọng sau khi đọc xong bài viết, các em sẽ thu thập thêm được nhiều thông tin bổ ích. Chúc các em luôn có những giờ học thật năng suất và đạt nhiều kết quả cao.

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!