Số phức là phần kiến thức quan trọng trong chương trình Toán Đại số cấp 3. Có thể nhận thấy, các dạng bài tập về số phức thường xuyên xuất hiện trong các đề kiểm tra hay đề thi. Để hiểu rõ hơn về số phức cũng như biết cách giải bài toán số phức bằng máy tính cầm tay, các em hãy đọc ngay bài viết bên dưới đây từ Team Marathon Education.
>>> Xem thêm: Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10
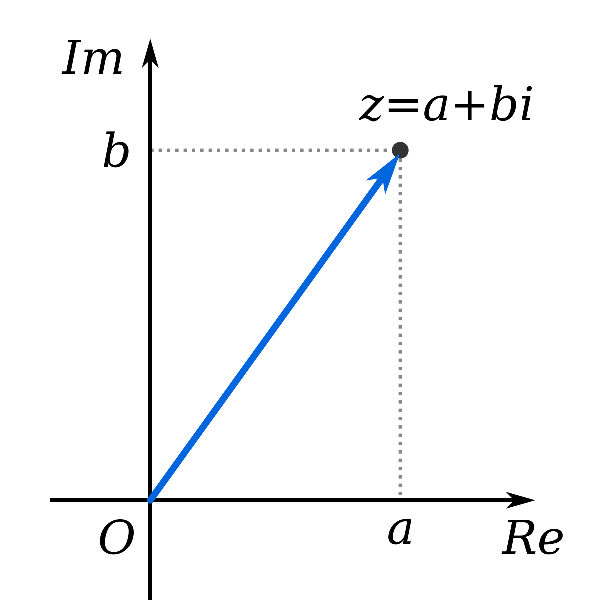
Cho một số phức xác định z = a+bi (với a, b là các số thực). Xét trong mặt phẳng phức Oxy, z sẽ được biểu diễn dưới dạng điểm M (a;b) hoặc bởi vectơ u = (a;b). Một điểm cần lưu ý ở đây đó chính là ở mặt phẳng phức, Ox sẽ được gọi là trục thực và Oy sẽ được gọi là trục ảo.
Khái niệm về môđun số phức z = a+bi có thể được hiểu là độ dài của vectơ u (a;b) biểu diễn số phức được đề cập.
\begin{aligned}
&\text{Kí hiệu: }|z|=\sqrt{a^2+b^2}\\
&\bull |z_1z_2|=|z_1|.|z_2|\\
&\bull ||z_1|-|z_2||\le |z_1+z_2| \le |z_1|+|z_2|\\
&\bull \left|\frac{z_1}{z_2}\right|=\frac{|z_1|}{|z_2|}
\end{aligned}
\begin{aligned}
&\text{Số phức liên hợp của số phức z = a+bi là }\overline{z}=a-bi\\
&\bull|z|=|\overline{z}|; \ \overline{z\mp z}'=\overline{z}\pm \overline{z'} \\&\ \ \ \ \ \overline{z.z'}=\overline{z}.\overline{z'};\ \overline{\left(\frac{z_1}{z_2}\right)}=\frac{\overline{z_1}}{\overline{z_2}}; \ z.\overline{z}=a^2+b^2\\
&\bull\text{Nếu z là số thực thì }z=\overline{z}\\
&\bull\text{Còn nếu z là số ảo thì }z=-\overline{z}
\end{aligned}
Dưới đây là một số phép tính giữa 2 số phức z1=a1+b1i và số phức z2=a2+b2i mà các em cần ghi nhớ:
\begin{aligned}
&\bull z^{-1}=\frac{1}{z^2}.\overline{z} \text{ với } z\not=0\\
&\bull \frac{z'}{z}=z'.z^{-1}=\frac{z'.z}{|z|^2}=\frac{z'.z}{z.\overline{z}}\\
&\bull \frac{z'}{z}=2 \Leftrightarrow z'=wz
\end{aligned}
z = x + yi là căn bậc hai của số phức w = a + bi ⇔ z2 = w ⇔ x2 – y2 = a và 2xy = b.
\begin{aligned}
&\footnotesize\text{Đặt }r=\sqrt{a^2+b^2},\ cos\varphi=\frac{a}{r},\ sni\varphi=\frac{b}{r} \text{ thì số phức }z=a+bi \text{ sẽ được biểu diễn}\\
&\footnotesize\text{dưới dạng: }z=r(cos\varphi+isin\varphi). \text{ Trong đó:}\\
&\footnotesize\ \ \ \bull \varphi\text{ là acgumen của số phức z}\\
&\footnotesize\ \ \ \bull z^n=r^n(cos(n\varphi)+isin(n\varphi))
\end{aligned}
Máy tính cầm tay sẽ là “trợ thủ đắc lực” giúp các em giải quyết các bài toán liên quan về số phức đơn giản hơn. Dưới đây là cách giải bài toán số phức bằng máy tính bỏ túi mới nhất mà các em cần biết.
Ngoài ra, Marathon Education cũng sẽ giới thiệu đến các em một số cách bấm phím với số phức qua bảng như sau:
| Tính năng | Cách bấm |
| Phần ảo (i) | Bấm phím ENG |
| Lấy Modun số phức (|z|) | Bấm Shift+hyp |
| Số phức liên hợp (z) | Bấm Shift+2+2 |
| Argument | Bấm Shift+2+1 |
| Lấy phần thực của số phức | Bấm Shift+2+3 |
| Lấy phần ảo của số phức | Bấm Shift+2+4 |
| Đổi sang dạng lượng giác | Bấm Shift+ mũi tên dưới +1 |
| Đổi sang dạng số | Bấm Shift+ mũi tên dưới +2 |
Để giúp các em hình dung cách bấm tốt hơn, Marathon Education có chia sẻ một số ví dụ sau:
Ví dụ 1: Tính z = (1 + 2i)3 + (3 – i)2
Ví dụ 2: Tìm modun của số phức
\begin{aligned}
&z = \left(\frac{3i+1}{2+i}\right)^2\\
&\bull\text{Bấm MODE 2.}\\
&\bull\text{Bấm }\left(\frac{3i+1}{2+i}\right)^2 \text{ thì sẽ được giá trị bằng 2.}
\end{aligned}
Ví dụ 3:
\text{Tìm }\overline{z}\text{ biết }z=\frac{3i-2}{i+1}
Ở bài này ta sẽ có 2 cách bấm máy, cụ thể như sau:
\footnotesize \text{Sau khi bấm MODE 2, ta tiếp tục bấm }\frac{3i-2}{i+1} \text{ sẽ được kết quả }\frac12+\frac52i.\text{ Vậy, giá trị }\overline{z}=\frac12-\frac52i.
\footnotesize \text{Nhập phép toán vào máy tính thì màn hình sẽ hiện là Conjg}\left(\frac{3i-2}{1+1}\right), \text{ được kết quả bằng }\frac12-\frac52i.
Tham khảo ngay các khoá học online của Marathon Education
Kiến thức về số phức không phải là quá khó. Chỉ cần dành nhiều thời gian rèn luyện, các em sẽ sớm “công phá” được dạng toán này từ A đến Z. Ngoài ra, các em có thể học online thêm nhiều kiến thức Toán – Lý – Hóa hữu ích khác trên website Marathon. Chúc các em luôn học tập tốt và đạt điểm cao trong các kì thi.
CÓ THỂ BẠN QUAN TÂM
