Lý thuyết, công thức về Bất đẳng thức bunhiacopxki
Bất đẳng thức Bunhiacopxki là một trong những nhánh quan trọng của bất đẳng thức Cauchy-Schwarz. Bất đẳng thức này này thường được sử dụng nhiều trong các bài toán chứng minh bất đẳng thức nâng cao. Các em hãy ùng Marathon Education tìm hiểu về công thức tính, cách chứng minh và bài tập bất đẳng thức Bunhiacopxki qua bài viết dưới đây.
Bất đẳng thức Bunhiacopxki là gì?

Bất đẳng thức Bunhiacopxki có tên gọi ban đầu bất đẳng thức Cauchy – Bunhiacopxki – Schwarz sau đó rút gọn lại gọi theo tên của nhà toán học người Nga Bunhiacopxki. Bất đẳng thức này do 3 nhà toán học nghiên cứu và phát triển. Trong lĩnh vực toán học, bất đẳng thức này được ứng dụng khá nhiều để giải các bài toán chứng minh bất đẳng thức và tìm cực trị.
Công thức bất đẳng thức Bunhiacopxki
Bất đẳng thức Bunhiacopxki dạng cơ bản:
\begin{aligned}
&(a^2+b^2)(c^2+d^2)\geq(ac+bd)^2\\
&\text{Dấu "=” xảy ra khi }ac = bd
\end{aligned}
Bất đẳng thức Bunhiacopxki dạng tổng quát:
Với hai bộ số (a1, a2,…,an) và (b1, b2,…,bn), ta có:
\begin{aligned}
&(a_1^2 + a_2^2 + … + a_n^2).(b_1^2 + b_2^2 + … + b_n^2) ≥ (a_1b_1 + a_2b_2 + … + a_nb_n)^2\\
&\text{Dấu “=” xảy ra khi } \frac{a_1}{b_1} = \frac{a_2}{b_2} =... = \frac{a_n}{b_n}\\
\end{aligned}
Nếu một số nào đó (i = 1, 2, 3,…, n) bằng 0 thì đẳng thức tương ứng bằng 0.
Ngoài ra:
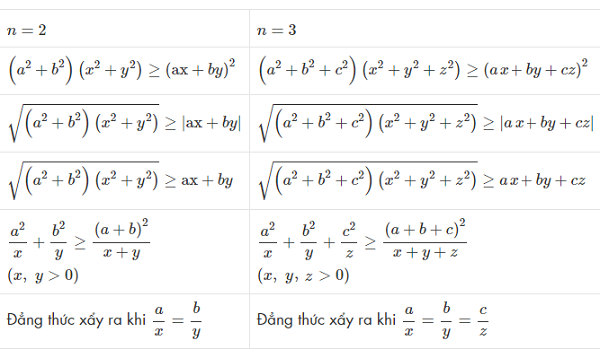
Hệ quả của bất đẳng thức Bunhiacopxki
Hệ quả 1
\small\text{Nếu }a_1x_1 +... + a_nx_n = C \text{ thì } min(x_1^2+...+x_n^2)=\frac{C}{a_1^2+...+a_n^2} \text{đạt được khi }\frac{x_1}{a_1} =... = \frac{x_n}{a_n}
Hệ quả 2
\begin{aligned}
&\small \text{Nếu } x_1^2 +...+ x_n^2 = C^2 \text{ (không đổi) thì:}\\
&\small \bull Max(a_1x_1+...+a_nx_n)=C.\sqrt{a_1^2+...+a_n^2} \text{ đạt được khi } a_1x_1 =... = a_nx_n\geq0.\\
&\small \bull Min(a_1x_1+...+a_nx_n)=-C.\sqrt{a_1^2+...+a_n^2} \text{ và dấu "=" xảy ra khi } a_1x_1 =... = a_nx_n\leq0.\\
\end{aligned}
Chứng minh bất đẳng thức Bunhiacopxki
Các em có thể chứng minh bất đẳng thức Bunhiacopxki như sau:
Ta có:
\begin{aligned}
&(a^2+b^2)(c^2+d^2)\geq(ac+bd)^2\\
&\Leftrightarrow(ac)^2 + (ad)^2 + (bc)^2 + (bd)^2 ≥ (ac)^2 + 2abcd + (bd)^2\\
&\Leftrightarrow (ad)^2 + (bc)^2 ≥ 2abcd\\
&\Leftrightarrow (ad)^2 - 2abcd + (bc)^2 ≥0\\
&\Leftrightarrow (ad - bc)^2 ≥ 0\text{ (luôn đúng)}
\end{aligned}
Bài tập bất đẳng thức Bunhiacopxki lớp 9
Bài tập 1: Cho các số a, b, c là các số thực dương bất kỳ. Chứng minh rằng:
\sqrt{\frac{a + b}{a + b + c}}+\sqrt{\frac{b + c}{a + b + c}}+\sqrt{\frac{c + a}{a + b + c}}\leq6
Hướng dẫn:
Áp dụng bất đẳng thức bunhiacopxki cho phân thức, ta có:
\begin{aligned}
&\footnotesize \sqrt{\frac{a + b}{a + b + c}}+\sqrt{\frac{b + c}{a + b + c}}+\sqrt{\frac{c + a}{a + b + c}}\\
&\footnotesize \Leftrightarrow 1.\sqrt{\frac{a + b}{a + b + c}}+1.\sqrt{\frac{b + c}{a + b + c}}+1.\sqrt{\frac{c + a}{a + b + c}}\leq\sqrt{(1+1+1)\left(\frac{a + b}{a + b + c}+\frac{b + c}{a + b + c}+\frac{c + a}{a + b + c}\right)}\\
&\footnotesize \Leftrightarrow \sqrt{\frac{a + b}{a + b + c}}+\sqrt{\frac{b + c}{a + b + c}}+\sqrt{\frac{c + a}{a + b + c}}\leq \sqrt{3.\left[\frac{2(a + b+c)}{a + b + c}\right]}\\
&\footnotesize \Leftrightarrow \sqrt{\frac{a + b}{a + b + c}}+\sqrt{\frac{b + c}{a + b + c}}+\sqrt{\frac{c + a}{a + b + c}}\leq \sqrt{3.2}=\sqrt6 \text{ (điều phải chứng minh)}\\
&\footnotesize\text{Dấu “=” xảy ra khi và chỉ khi các giá trị a = b = c}
\end{aligned}\\
Bài tập 2: Tìm giá trị lớn nhất (max) của biểu thức sau:
P=\sqrt{x-2}+\sqrt{4-x}
Hướng dẫn:
\begin{aligned}
&\footnotesize P=\sqrt{x-2}+\sqrt{4-x}\\
&\footnotesize \text{Điều kiện: }2 ≤ x ≤ 4\\
&\footnotesize \text{Áp dụng bất đẳng thức bunhiacopxki, ta có:}\\
&\footnotesize (1.\sqrt{x -2} + 1.\sqrt{4 -x})^2 ≤ (1^2 + 1^2).(x - 2 + 4 - x) = 2^2 = 4\\
&\footnotesize⟹ P^2 ≤ 4\\
&\footnotesize ⟺ -2 ≤ P ≤ 2\\
&\footnotesize \text{P đạt giá trị lớn nhất khi }P = 2 ⟺ \frac{1}{\sqrt{x -2}} = \frac{1}{\sqrt{4 -x}} ⟺ x - 2 = 4 - x ⟺ x = 3 (TMĐK)\\
&\footnotesize \text{Vậy }P_{max} = 2 ⟺ x = 3
\end{aligned}
Bài tập 3: Cho các số a, b, c là các số thực dương tùy ý. Chứng minh rằng:
\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^2}{a+b}\geq \frac{a+b+c}{2}
Hướng dẫn:
Áp dụng bất đẳng thức bunhiacopxki.
Ta được:
\begin{aligned}
&\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^2}{a+b}\geq\frac{(a+b+c)^2}{(a+b)+(b+c)+(c+a)}=\frac{(a+b+c)^2}{2(a+b+c)}=\frac{a+b+c}{2}\\
&\text{Đẳng thức xảy ra khi và chỉ khi các số a = b = c}
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Bất đẳng thức Bunhiacopxki thường được áp dụng nhiều trong các bài tập chứng minh bất đẳng thức và tìm cực trị. Do đó, các em cần phải nắm vững khái niệm, công thức tính, cách chứng minh bất đẳng thức Bunhiacopxki và làm nhiều dạng bài tập khác nhau để nâng cao kỹ năng giải toán của bản thân.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






