Lý thuyết Toán 10 hàm số bậc hai và cách giải bài tập
Toán 10 hàm số bậc hai là một trong những kiến thức Toán quan trọng ở bậc học trung học phổ thông. Do đó, các em cần nắm vững những nội dung trọng tâm liên quan đến chủ đề này như định nghĩa, cách xét dấu, đồ thị của hàm số bậc hai,… cùng các dạng bài tập thường gặp. Team Marathon Education đã tổng hợp và chia sẻ đến các em những kiến thức này qua bài viết dưới đây. Hy vọng rằng bài viết sẽ có ích cho các em trong quá trình học tập.
Hàm số bậc hai là gì?
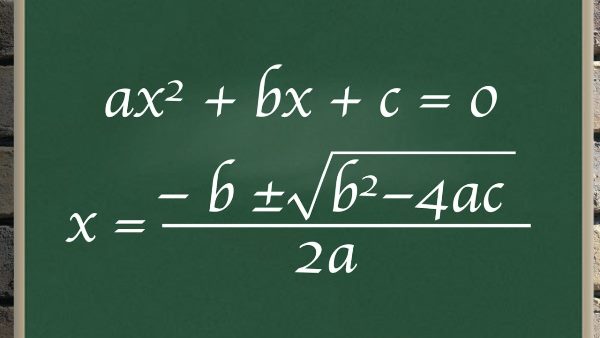
Định nghĩa hàm số bậc hai
- Hàm số bậc hai là hàm số có dạng y = ax2 + bx + c. Trong đó: a, b, c là những hằng số cho trước và a ≠ 0.
- Tập xác định là D = R.
- Hàm số y = ax2 (a ≠ 0) cũng là một dạng hàm số bậc hai có đồ thị là một đường cong Parabol.
Đồ thị của hàm số bậc hai
Ôn tập lại đồ thị y = ax2 (a ≠ 0)
- Đồ thị hàm số bậc hai này luôn đi qua gốc tọa độ O (0;0).
- Parabol luôn đối xứng qua trục tung.
- Parabol có bề lõm hướng lên trên khi a>0 và hướng xuống dưới khi a<0.
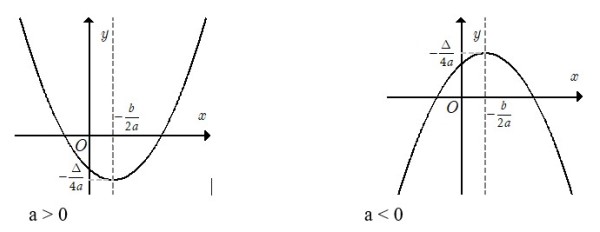
Đồ thị hàm số y = ax2 + bx + c (a ≠ 0)
Ta có:
\begin{aligned}
&ax^2+bx+c=a\left(x^2+2\frac{b}{2x}+\frac{b^2}{4a^2}\right)-\frac{b^2}{4a^2}+c\\
&=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}\\
\end{aligned}
Nếu ta đặt:
\Delta=b^2-4ac,\ p=-\frac{b}{2a},\ q=-\frac{\Delta}{4a}
Hàm số y = ax2 + bx + c (a ≠ 0) sẽ trở thành y = a(x – p)2 + q.
Vì vậy:
\begin{aligned}
&\footnotesize\text{Đồ thị hàm số bậc hai } y = ax^2 + bx + c \ (a ≠ 0)\text{ là một Parabol có đỉnh }I\left(-\frac{b}{2a};-\frac{\Delta}{4a}\right)\text{nhận đường thẳng}\\
&\footnotesize x=-\frac{b}{2a} \text{ là trục đối xứng và bề lõm hướng lên trên khi a > 0, bề lõm hướng xuống dưới khi a < 0.}
\end{aligned}
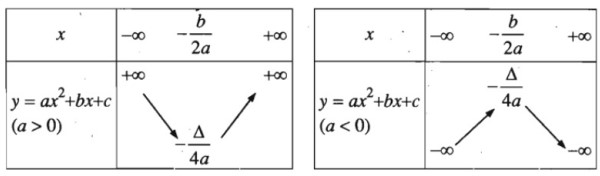
Sự biến thiên của hàm số bậc hai
\begin{aligned}
&\footnotesize\bull\text{Khi a dương, hàm số đồng biến trên khoảng }\left(-\frac{b}{2a};+∞\right), \text{ nghịch biến trên khoảng }\left(-∞;-\frac{b}{2a};\right)\text{ và có}\\
&\footnotesize\text{giá trị nhỏ nhất là }-\frac{\Delta}{4a} \text{ khi }x=-\frac{b}{2a}.\\
&\footnotesize\bull\text{Khi a âm, hàm số nghịch biến trên khoảng }\left(-\frac{b}{2a};+∞\right), \text{ đồng biến trên khoảng }\left(-∞;-\frac{b}{2a};\right)\text{ và có}\\
&\footnotesize\text{giá trị lớn nhất là }-\frac{\Delta}{4a} \text{ khi }x=-\frac{b}{2a}.\\
\end{aligned}
>>> Xem thêm: Lý Thuyết Toán 10 Dấu Của Tam Thức Bậc Hai Và Cách Xét Dấu
Các dạng bài tập về hàm số bậc hai thường gặp
Dạng 1: Xác định hàm số bậc hai dạng y = ax2 + bx +c
Cách làm
- Gọi hàm số bậc hai cần tìm có dạng y = ax2 + bx + c (a ≠ 0)
- Dựa vào giả thiết trong đề bài để thiết lập những mối tương quan và tiến hành giải hệ phương trình với các ẩn a, b, c. Sau đó, các em suy ra hàm số cần tìm.
Ví dụ: Xác định Parabol (P) y = ax2 + bx + c (a ≠ 0). Biết rằng (P) đi qua điểm A(2;3) và có đỉnh I(1;2)
Bài giải:
\begin{aligned}
&A ∈ (P) \text{ nên } 3 = 4a + 2b + c\ (1)\\
&(P) \text{ có đỉnh }I(1;2) \text{ nên }-\frac{b}{2a}=1\Leftrightarrow2a+b=0\ (2)\\
&I ∈ (P) \Leftrightarrow 2=a+b+c\ (3)\\
&\text{Từ (1), (2), (3), ta có: } \begin{cases}4a+2b+c=3\\2a+b=0\\a+b+c=2\\
\end{cases}\Leftrightarrow
\begin{cases}a=1\\b=-2\\c=3
\end{cases}\\
&\text{Vậy (P) cần tìm là: }y=x^2-2x+3
\end{aligned}
Dạng 2: Lập bảng biến thiên và vẽ đồ thị hàm số
Cách làm
Các bước để vẽ đồ thị hàm số bậc hai y = ax2 + bx + c (a ≠ 0):
\begin{aligned}
&\footnotesize\bull \ \text{Bước 1: Tìm tọa độ đỉnh }I\left(-\frac{b}{2a};-\frac{\Delta}{4a}\right).\\
&\footnotesize\bull \ \text{Bước 2: Tìm trục đối xứng của đồ thị theo công thức }x=-\frac{b}{2a}.\\
&\footnotesize\bull \ \text{Bước 3: Tùy thuộc vào từng hàm số, các em tìm hoành độ và tung độ của các điểm mà đồ thị hàm số bậc }\\
&\footnotesize\text{hai giao nhau với trục hoành và trục tung (nếu có). Ngoài điểm giao nhau, tìm thêm một số điểm đặc biệt của}\\
&\footnotesize\text{đồ thị như điểm đối xứng của các điểm cắt,... giúp đồ thị vẽ một cách chính xác nhất.}\\
&\footnotesize\bull \ \text{Bước 4: Tiến hành vẽ đồ thị theo các điểm đã xác định được.}
\end{aligned}
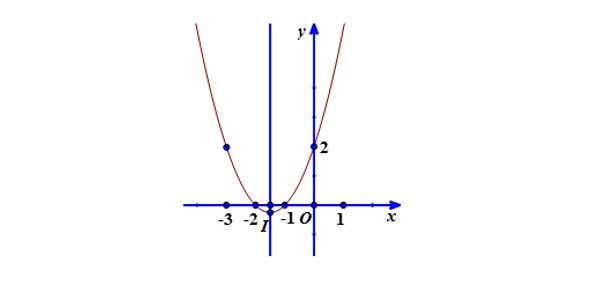
Ví dụ: Vẽ đồ thị hàm số y = x2 + 3x + 2
Bài giải:
Ta có:
-\frac{b}{2a}=-\frac{3}{2}\ ,\ -\frac{\Delta}{4a}=-\frac{1}{4}
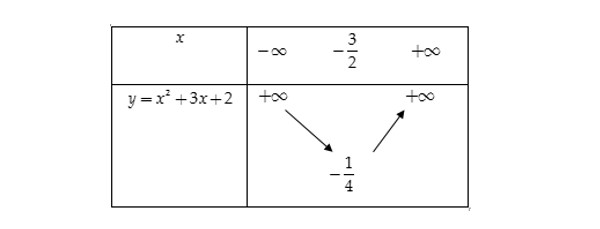
Bảng biến thiên:
\begin{aligned}
&\footnotesize\text{Suy ra đồ thị hàm số }y = x^2+3x+2 \text{ có đỉnh là }I\left(-\frac{3}{2};-\frac{1}{4}\right) \text{ và đi qua các điểm A(-2;0), B(-1;0), C(0;2),}\\
&\footnotesize\text{D(-3;2)}.\\
&\footnotesize\text{Đồ thị của hàm số nhận đường thẳng }x=-\frac{3}{2} \text{ làm trục đối xứng và có bề lõm hướng lên trên.}
\end{aligned}
Dạng 3: Tìm giá trị cực đại và giá trị cực tiểu của hàm số
Cách làm
\begin{aligned}
&\footnotesize\text{Dựa theo đồ thị hoặc bảng biến thiên của hàm số } y = ax^2 + bx + c\ (a ≠ 0) \text{các em xác định các điểm max và }\\
&\footnotesize\text{min của hàm số trong khoảng giá trị ⦍a;b⦎ tại }x = a, x = b\text{ hoặc }x=-\frac{b}{2a}.
\end{aligned}
Dạng toán này thuộc dạng nâng cao và thường khá ít gặp trong chương trình Toán 10 hàm số bậc hai. Do đó, Marathon chỉ giới thiệu sơ qua về phương pháp giải để các em nắm bắt.
Dạng 4: Tìm tọa độ giao điểm
Cách làm
Muốn giải được bài toán tìm tọa độ giao điểm của hai đồ thị f(x) và g(x). Các em giải phương trình hoành độ giao điểm f(x) = g(x) (1)
- Để tìm tung độ giao điểm, các em thay nghiệm x vào y = f(x) hoặc y = g(x) để tính y
- Trường hợp (1) có n nghiệm thì hai đồ thị có n điểm chung.
Ví dụ: Tìm tọa độ giao điểm của đồ thị bậc hai và đường thẳng sau:
(P): y = x2 – 2x – 1 và d: y = x – 1
Bài giải:
Xét phương trình tọa độ giao điểm của (P) và (d):
\begin{aligned}
&\bull x^2 - 4x - 2 = -2x - 2\\
&⇔ 2x^2 - 2x = 0\\
&⇔x= 1 \text{ hoặc } x = 0\\
&\bull x = 0 ⇒ y(0) = 0 - 1 = -1\\
&\bull x = 1 ⇒ y(1) = 1 - 1 = 0\\
&\text{Vậy tọa độ giao điểm cần tìm là }(0;-1) \text{ và }(1;0).
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Với những thông tin mà Marathon Education đã chia sẻ ở trên, hy vọng các em đã có thể tự mình làm tốt các bài tập về Toán 10 hàm số bậc hai cũng như vẽ đồ thị nhanh chóng. Ngoài việc ghi nhớ các kiến thức trọng tâm, các em hãy thường xuyên làm bài tập.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!
>> Có thể bạn quan tâm:
- Cách vẽ đồ thị hàm số lớp 10 – bài tập kèm giải chi tiết 2023
- Lý thuyết Hàm số và đồ thị – SGK Toán 10 Cánh Diều 2023
- Tổng quan lý thuyết về hàm số 10, các dạng bài tập hàm số 2023
- Ma trận đề thi THPT quốc gia 2023 cập nhật các môn






