3 Cách Giải Phương Trình Logarit Nhanh Và Chính Xác Nhất
Lý thuyết về phương trình logarit
Định nghĩa về phương trình logarit
Phương trình logarit là khi cơ số a dương và khác 1 phương trình có dạng gọi là phương trình logarit cơ bản: loga x = b ⇔ x = ab (0 < a ≠ 1).
- loga f(x) = loga g(x)
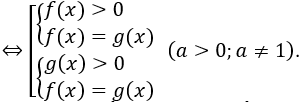
Xem chi tiết tại file: https://drive.google.com/
Các dạng phương trình logarit
Một số phương trình logarit cơ bản (điều kiện: 0 < a ≠ 1):
\begin{aligned}
&\small \bull log_ax=b ⟺ x=a^b\\
&\small \bull log_af(x)=log_ag(x) ⟺ \begin{cases}f(x),\ g(x)>0\\f(x)=g(x) \end{cases}\\
&\small \bull log_{f(x)}g(x)=b⟺\begin{cases}0< f(x) \not =1\\g(x)=f(x)^b \end{cases}\\
&\small \bull log_af(x) \ge log_ag(x)\ (1) \\
&\small \ \ \ \circ \text{Nếu a > 1 thì (1) }⟺ \begin{cases}f(x) \ge g(x)\\ g(x)>0 \end{cases}\\
&\small \ \ \ \circ \text{Nếu 0 < a < 1 thì (1) }⟺ \begin{cases}f(x) \le g(x)\\ f(x)>0 \end{cases}\\
&\small \bull \text{Chú ý: } log_af(x) \text{ có nghĩa }⟺\begin{cases}f(x)>0\\0 < a \not= 1 \end{cases}\\
\end{aligned}
Ngoài ra, các em cũng cần nắm vững các công thức liên quan về Logarit và lũy thừa dưới đây:

Cách giải phương trình logarit
Cách 1: Phương pháp đưa về cùng cơ số
Để giải phương trình logarit các em có thể dùng phương pháp đưa về cùng cơ số. Cụ thể:
- Bước 1: Xác định điều kiện của phương trình (nếu có)
- Bước 2: Vận dụng tất cả định nghĩa và tính chất của Logarit để đưa các Logarit có mặt trong phương trình về cùng một cơ số
- Bước 3: Tiến hành biến đổi phương trình về các dạng phương trình logarit cơ bản để giải
- Bước 4: Kiểm tra điều kiện và kết luận để kết thúc bài toán sau khi giải phương trình
Ví dụ:
Giải phương trình logarit sau: log2x + log3x + log4x = log20x
Hướng dẫn giải:
\begin{aligned}
&\text{ĐKXĐ: }x>0\\
&log_2x + log_3x + log_4x = log_{20}x\\
\Leftrightarrow\ &log_2x+\frac{log_2x}{log_23}+\frac{log_2x}{log_24}+\frac{log_2x}{log_220}=0\\
\Leftrightarrow\ &log_2x\left(1+\frac{1}{log_23}+\frac12-\frac{1}{log_220} \right)=0\\
\Leftrightarrow\ &log_2x\left(\frac32+log_32-log_{20}2\right)=0\\
\Leftrightarrow\ &log_2x=0\\
\Leftrightarrow\ &x=1\\
&\text{Vậy phương trình có nghiệm }x=1.
\end{aligned}
>>> Xem thêm: Bất Phương Trình Mũ Và Bất Phương Trình Lôgarit – Lý Thuyết Toán 12
Cách 2: Phương pháp đặt ẩn phụ
Để giải phương trình logarit bằng cách đặt ẩn phụ, các em có thể thực hiện theo các phương pháp sau:
\begin{aligned}
&f[log_ag(x)]=0\ (0< a \not=1)\\
&\Leftrightarrow \begin{cases}t=log_ag(x)\\f(t)=0 \end{cases}
\end{aligned}
Công thức đổi cơ số logarit:
log_bx=\frac{log_ax}{log_ab} \Rightarrow log_ab=\frac{1}{log_ba}\ \forall a,b,x>0 \text{ và }a,b \not= 1
Ví dụ:
Giải phương trình sau:
\sqrt{log_9x+1}+\sqrt{log_3x+3}=5
Hướng dẫn giải:
\begin{aligned}
&\text{ ĐKXĐ: }\begin{cases}x>0\\log_9x+1\ge0\\log_3x+3\ge 0 \end{cases}\\
&\text{ Đặt }t=log_3x\\
&\sqrt{log_9x+1}+\sqrt{log_3x+3}=5\\
\Leftrightarrow \ &\sqrt{\frac12t+1}+\sqrt{t+3}=5 \ (ĐK: t\ge -2)\\
\Leftrightarrow \ &\frac12t+1+t+3+2\sqrt{\left( \frac12t+1\right)\left( t+3\right)}=25\\
\Leftrightarrow \ &\sqrt{\frac12t^2+\frac52t+3}=21-\frac32t\\
\Leftrightarrow \ &\begin{cases}-2\le t \le 14\\t^2-292t+1716=0 \end{cases}\\
\Leftrightarrow \ &t=6 \text{ (thỏa điều kiện)}\\
\Leftrightarrow \ &x=64\\
&\text{Vậy nghiệm của phương trình là }x=64.
\end{aligned}
Cách 3: Phương pháp mũ hóa
Khi gặp dạng phương trình còn có chứa cả logarit và mũ, các em có thể áp dụng phương pháp mũ hóa sau đó logarit hóa 2 vế để giải.
Ví dụ:
Giải phương trình: log2(2x + 6) = 2x + 1
Hướng dẫn giải:
\begin{aligned}
&log_2(2^x + 6) = 2x + 1\\
\Leftrightarrow\ & 2^{log_2(2^x+6)}=2^{2x+1}\\
\Leftrightarrow\ & 2^x+6=2.2^x\\
\Leftrightarrow\ & 2.2^x-2^x-6=0\\
\Leftrightarrow\ & \left[ \begin{array}{c}2^x=-3\\2^x=2 \end{array}\right.\\
\Leftrightarrow\ & x=1\\
&\text{Vậy phương trình có nghiệm duy nhất là }x=1.
\end{aligned}
Tham khảo ngay các khoá học online của Marathon Education
Trên đây là những chia sẻ về các dạng phương trình logarit thường gặp và các phương pháp giải chi tiết. Hy vọng những nội dung này sẽ giúp ích cho các em trong quá trình học tập và ôn thi.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






