Lý Thuyết Bất Đẳng Thức Tam Giác: Quan Hệ Giữa 3 Cạnh Trong 1 Tam Giác
Hình tam giác là một trong những hình học phổ biến và có nhiều công thức cần nhớ khi làm bài tập. Trong đó, bất đẳng thức tam giác là lý thuyết quan trọng giúp các em giải được các dạng bài tập liên quan đến quan hệ giữa 3 cạnh trong 1 tam giác. Vậy bất đẳng thức tam giác là gì, các yếu tố trong tam giác có quan hệ như thế nào? Các em hãy cùng Marathon Education tìm hiểu qua bài viết sau đây.
>>> Xem thêm:
- Chia Sẻ Bí Quyết Học Tốt Hình Học Không Gian Lớp 11
- Tổng Hợp 13 Dạng Hình Học Không Gian Thường Gặp Và Cách Giải
Bất đẳng thức tam giác là gì? Quan hệ giữa 3 cạnh trong 1 tam giác
Định lý bất đẳng thức tam giác
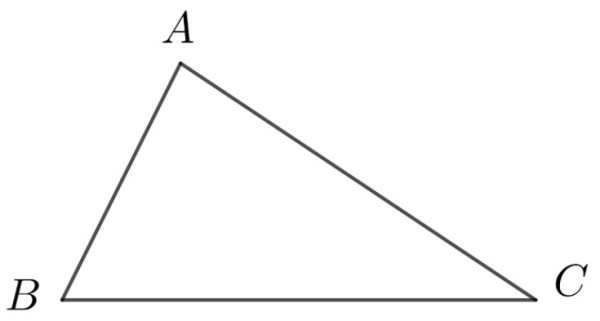
Trong một tam giác bất kỳ, tổng độ dài hai cạnh bao giờ cũng lớn hơn độ dài cạnh còn lại.
Ví dụ: Trong tam giác ABC với 3 cạnh lần lượt là AB, AC và BC ta có:
- AB + AC > BC
- AB + BC > AC
- AC + BC > AB
Hệ quả của bất đẳng thức tam giác
Trong một tam giác bất kỳ, hiệu độ dài hai cạnh bao giờ cũng nhỏ hơn độ dài cạnh còn lại.
Ví dụ: Trong tam giác ABC, ta có: |AB − AC| < BC < AB + AC
>>> Xem thêm: Tổng Hợp Các Kí Hiệu Trong Toán Học Phổ Biến Đầy Đủ Và Chi Tiết
Chứng minh bất đẳng thức tam giác
1. Cho tam giác ABC, chứng minh rằng: AB + AC > BC
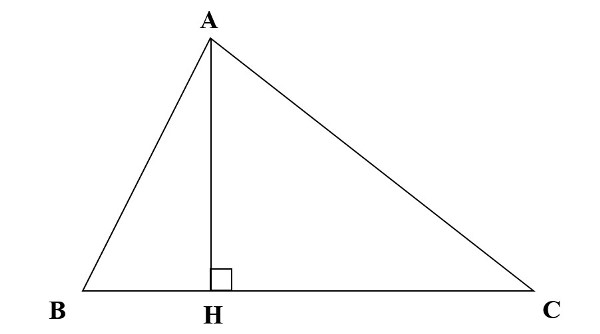
Bài giải:
Kẻ AH ⊥ BC (H ∈ BC)
=> AB > HB (AB là cạnh huyền trong tam giác vuông ABH)
AC > HC (AC là cạnh huyền trong tam giác vuông ACH)
Do đó: AB + AC > HB + HC
⇔ AB + AC > BC
Chứng minh tương tự với cạnh AC, AB ta có AB + BC > AC và AC + BC > AB.
2. Cho tam giác ABC, chứng minh rằng: AB > BC – AC
Ta có: AB + AC > BC (định lý bất đẳng thức tam giác)
=> AB > BC – AC
Chứng minh tương tự, ta có: AC > AB – BC
BC > AB – AC
AB > AC – BC
AC > BC – AB
BC > AC – AB
Vậy, trong một tam giác, độ dài một cạnh bao giờ cũng nhỏ hơn tổng và lớn hơn hiệu độ dài hai cạnh còn lại.
Quan hệ giữa các yếu tố trong tam giác
Quan hệ giữa góc và cạnh đối diện
Định lý 1: Trong một tam giác bất kỳ, khi góc đối diện với cạnh lớn hơn là góc lớn hơn.
\triangle ABC, \ AC>AB \Rightarrow \widehat{B}>\widehat{C}
Định lý 2: Trong một tam giác bất kỳ, khi cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
\triangle ABC,\ \widehat{B}>\widehat{C}\Rightarrow AC>AB
Quan hệ giữa đường vuông góc và đường xiên
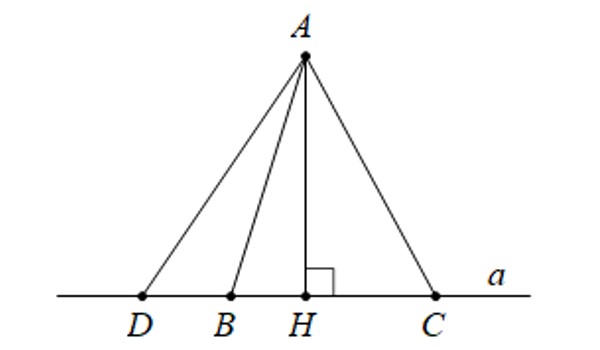
Định lý: Trong các đường xiên và đường vuông góc được kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Quan hệ giữa các đường xiên và hình chiếu của chúng
Định lý: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó nếu:
- Đường xiên nào có hình chiếu lớn hơn là đường xiên lớn hơn
- Đường xiên nào lớn hơn là đường xiên có hình chiếu lớn hơn
- Nếu hai đường xiên bằng nhau thì có hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
>>> Xem thêm: Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10
Tham khảo ngay các khoá học online của Marathon Education
Qua bài viết trên, Marathon Education đã cung cấp cho các em kiến thức về bất đẳng thức tam giác, quan hệ giữa 3 cạnh trong 1 tam giác và quan hệ giữa các yếu tố trong tam giác. Hy vọng rằng sau khi đọc xong bài viết, các em có thể nắm vững được phần nội dung này.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






