Đạo Hàm Là Gì? Ý Nghĩa Và Các Công Thức Tính Đạo Hàm Thường Gặp

Trong chương trình Toán học trung học phổ thông, đạo hàm của hàm số là một nội dung vô cùng quan trọng. Vậy đạo hàm là gì? Những công thức tính đạo hàm nào hay gặp nhất? Trong bài viết này, Team Marathon Education sẽ tổng hợp cho các em lý thuyết đạo hàm là gì và các công thức tính đạo hàm thường gặp.

>>> Xem thêm:

• Toán 12 Nguyên Hàm – Lý Thuyết, Công Thức Và Các Dạng Bài Tập
• Bảng Nguyên Hàm Và Công Thức Nguyên Hàm Đầy Đủ, Chi Tiết

Đạo hàm là gì?

Để giải các bài toán về đạo hàm, các em cần hiểu rõ khái niệm đạo hàm là gì. Theo toán học giải tích, đạo hàm thực chất là một đại lượng được dùng để mô tả sự biến thiên của hàm số tại một điểm nào đó.

Định nghĩa

\begin{aligned}
&\footnotesize\text{Cho hàm số y = f(x) được xác định trên khoảng (a;b) và }x_0 \text{ ∈ (a;b).}\\
&\footnotesize\text{Giới hạn hữu hạn của tỉ số }\frac{f(x)-f(x_0)}{x-x_0} \text{ (nếu có) khi x} \to x_0 \text{ được gọi là}\\
&\footnotesize\text{đạo hàm của hàm số f(x) tại }x_0. \text{ Ký hiệu đạo hàm là }f'(x_0)\text{ hay }y'(x_0).
\end{aligned}

Như vậy:

f'(x_0)=\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}

Đặt: x – x₀ = ∆x và ∆y = f(x₀+∆x) – f(x₀) thì các em sẽ có được:

f'(x_0)=\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}

Trong đó:

• ∆x là số gia của đối số tại x_0.
• ∆y được gọi là số gia tương ứng của hàm số.

Cách tính đạo hàm dựa trên định nghĩa

Khi các em đã biết được đạo hàm là gì, nội dung này cũng sẽ trở nên đơn giản hơn. Dựa vào định nghĩa trên, các em có thể tính đạo hàm của hàm số theo các bước sau:

\begin{aligned}
&\footnotesize\text{Bước 1: Tính } Δy = f(x0+Δx) − f(x0)\text{ với Δx là số gia của số đối tại }x_0.\\
&\footnotesize\text{Bước 2: Lập tỉ số }\frac{\Delta y}{\Delta x}.\\
&\footnotesize\text{Bước 3: Tính}\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}
\end{aligned}

Nhận xét: Nếu các em thay x₀ = x thì sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số y = f(x) tại điểm x ∈ (a;b).

Quan hệ giữa tính liên tục và sự tồn tại đạo hàm

Định lý: Nếu hàm số y = f(x) có đạo hàm tại x₀ thì nó liên tục tại x_0.

Lưu ý: Nếu hàm số y = f(x) gián đoạn tại x₀ thì nó không có đạo hàm tại điểm x₀. Tuy nhiên, một hàm số liên tục tại một điểm cũng có thể không có đạo hàm tại điểm đó.

Ý nghĩa của đạo hàm là gì?

Ý nghĩa hình học

Cho hàm số y = f(x) có đồ thị (C) thì f’(x₀) là hệ số góc tiếp tuyến của đồ thị (C) của hàm số y = f(x) tại điểm M₀ (x₀; f(x₀)).

Lúc này, phương trình tiếp tuyến của đồ thị tại điểm M₀ (x₀;f(x₀)) sẽ là:

y - f(x_0) = f'(x_0)(x-x_0)

Ý nghĩa vật lý

Ngoài ý nghĩa hình học thì đạo hàm còn có ý nghĩa vật lý. Vậy ý nghĩa vật lý của đạo hàm là gì? 

Trong một chuyển động thẳng, vận tốc tức thời của chuyển động tại thời điểm t có thể được tính bằng công thức v(t) = s'(t).

Các công thức tính đạo hàm thường gặp

Sau khi biết được đạo hàm là gì, các em hãy ghi nhớ một số công thức tính đạo hàm thường gặp sau để áp dụng giải các bài tập.

Công thức tính đạo hàm hàm hợp:

\begin{array}{ccc}
(u+v)'=u'+v' & (uv)'=u'v+uv'&\left( \frac{u}{v}\right)'=\frac{u'v-uv'}{v^2}\\
y'_x=y'_u.u'_x&(ku)'=k.u'&\left( \frac{k}{u}\right)'=\frac{k.u'}{u^2}
\end{array}

Công thức tính đạo hàm các hàm số sơ cấp:

Công thức tính đạo hàm cấp cao:

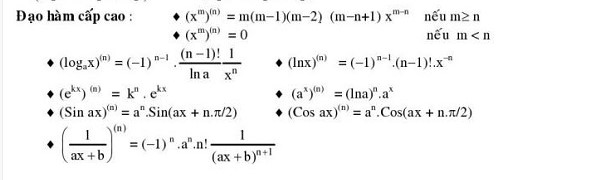
Các quy tắc tính đạo hàm:

Công thức tính đạo hàm của một số phân thức hữu tỉ thường gặp:

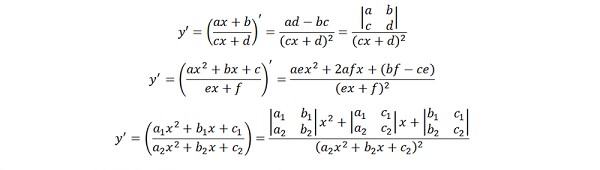
Tham khảo ngay các khoá học online của Marathon Education

Qua bài viết này, Marathon Education đã tổng hợp những nội dung cơ bản để các em hiểu rõ đạo hàm là gì và các công thức tính đạo hàm thường gặp. Đây là kiến thức trọng tâm để chuẩn bị cho kỳ thi THPTQG. Các em hãy chú ý học thuộc, nắm chắc các công thức để giải đúng các bài tập và dễ dàng vượt qua các kỳ thi. 

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!